Empirical Two-Ray Model
The empirical two-ray model (ETR) model computes the path loss to each pixel based on the assumption that the direct ray and the ground-reflected ray would exist.
There is no check if the rays do exist or if they are shadowed. The visibility check is only made in the deterministic two ray model (DTR) which considers rays only if they are not shadowed.
Click and click the Computation tab.
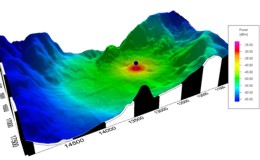
The figure shows a prediction with the ETR model in a hilly scenario. The received power is predicted for all pixels independent of the visibility status between transmitter and receiver. The predicted values for the path loss do not depend on the LOS or NLOS status. To include an additional loss for all pixels which have no LOS to the transmitter, the ETR must be combined with the knife edge diffraction model to include the diffractions at the topographical obstacles.
Settings
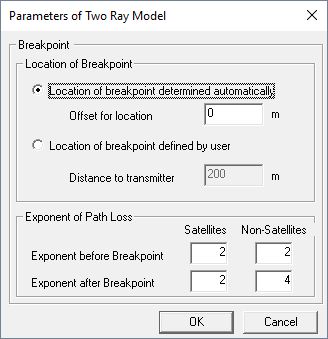
The Breakpoint describes the physical phenomenon that further than a certain distance the received power decreases with instead of which is valid for the free space propagation. This is due to the superposition of the direct ray with a ground reflected contribution.
- Exponent before breakpoint / Exponent after breakpoint
- These two exponents influence the calculation of the distance-dependent attenuation. The default values are 2 for the exponent before the breakpoint and 4 for the exponent after the breakpoint.
- (Additional) breakpoint offset
- The breakpoint distance depends on the height of the transmitter and receiver as well as the wavelength (the initial value is calculated according to ). This value can be modified by setting an additional offset (in meters).
Monte Carlo simulation methodology for the use in sharing and compatibility studies between different radio services or systems, section 6.1, published June 2017.