/MAT/LAW88

Unloading can be represented using an unloading function or by providing hysteresis and shape factor inputs to a damage model based on energy. This law is only compatible with solid elements.

Format

(1)	(3)	(5)	(7)	(8)	(9)
/MAT/LAW88/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
$ν$	`K`	`F`_cut	`F`_smooth	`N`_L
`fct_ID`_unL	`Fscale`_unL	`Hys`	`Shape`		`Tension`

If N_L > 0, define N_L functions per line

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_Li		`Fscale`_Li		${\dot{ε}}_{L i}$

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
$ν$	Poisson ratio. For incompressible materials 0.495 is maximum value. Default = 0.495 (Real)
`K`	Bulk modulus. (Real)	$[Pa]$
`F`_cut	Cutoff frequency for strain rate filtering. Default = 10³⁰ (Real)	$[Hz]$
`F`_smooth	Smooth strain rate option flag. = 0 (Default) No strain rate smoothing. = 1 Strain rate smoothing active. (Integer)
`N`_L	Number of loading stress strain curve. (Integer)
`fct`_unL	Unloading engineering stress versus engineering strain function identifier. 3 (Integer)
`Fscale`_unL	Unloading function scale factor. Default = 1.0 (Real)	$[Pa]$
`Hys`	Hysteresis unloading factor. Ignore if, unloading function is used. 3 0.0 ≤ `Hys` ≤ 1.0 Default = 0.0 (Real)
`Shape`	Shape factor. Ignored if, unloading function is used. 3 Default = 1.0 (Real)
`Tension`	Unloading rate effects option flag. 4 = -2 Unloading curve is used and should have a closed loop (both and compression and tensile) with the quasi-static loading curve. There is no strain rate dependency for this formulation. = -1 or 1 Unloading curve is used if `fct_ID`_unL is defined. Otherwise, `Hys` and `Shape` parameters are used. = 0 (Default) Set to 1. Otherwise, the quasi-static loading curve is used for unloading. (Integer)
`fct_ID`_Li	Loading function identifier defining engineering stress versus engineering strain for i^th strain rate function. (Integer)
${\dot{ε}}_{L i}$	Strain rate for i^th loading engineering stress versus engineering strain function. (Real)	$[\frac{1}{s}]$
`Fscale`_Li	Scale factor for i^th loading function. Default = 1.0 (Real)	$[Pa]$

Example (Rubber)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW88/1/1
rubber
#              RHO_I        
                1E-6 		
#                 NU                   K               F_cut  F_smooth       N_L      
                .495               19.93                   0                   1
#fctID_Unl                 Fscale_unload                 HYs               Shape   Tension     
         1                            1.                  0.                  0.         0
#fctID_l                     Fscale_load          Eps_._load
         1                            1.                  0.
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
function 1
#                  X                   Y
           -8.51E-01           -3.55E+01	
           -7.76E-01           -1.10E+01	
           -7.02E-01           -4.83E+00	
           -6.01E-01           -2.06E+00	
           -5.00E-01           -1.05E+00	
           -4.05E-01           -5.98E-01	
           -3.04E-01           -3.33E-01	
            0.00E+00            0.00E+00	
            4.05E-01            1.53E-01	
            8.50E-01            2.37E-01
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

This model utilizes an Ogden material formulation. Material parameters are directly derived from the input stress strain curves from uniaxial tests for different strain rates. The material is assumed to be nearly incompressible with Poisson’s ratio = 0.495.
Strain rate effects can be modeled by including loading engineering stress strain test data at different strain rates fct_ID_Li. This can be easier than calculating viscous parameters for traditional hyperelastic material models. When using stress strain curves at different strain rates, the following suggestions are recommended:
- The stress strain curve should be monotonic increasing and smooth. The derivative of the stress strain curve should be smooth.
- Enable strain rate smoothing by defining, F_smooth =1 with F_cut =500 Hz.
Unloading can be represented using an unloading function, Fscale_unL, or by providing hysteresis, Hys, and shape factor, Shape, inputs to a damage model based on energy.
- The unloading behavior does not consider the strain rate dependency.
- Unloading hysteresis stress is computed from the quasi-static behavior with:(1)
  $σ = (1 - D) σ$
  
  with(2)
  $D = (1 - H y s) (1 - {(\frac{W_{c u r}}{W_{\max}})}^{S h a p e})$
Where,

$W_{c u r}$

Current energy

$W_{\max}$

Maximum energy corresponding to the quasi-static behavior
The loading and unloading curves are defined with positive stress and strain in tensile and negative stress and strain in compression.
The following curves are needed according to Tension flag:
- Tension = -1, 0, or 1
  
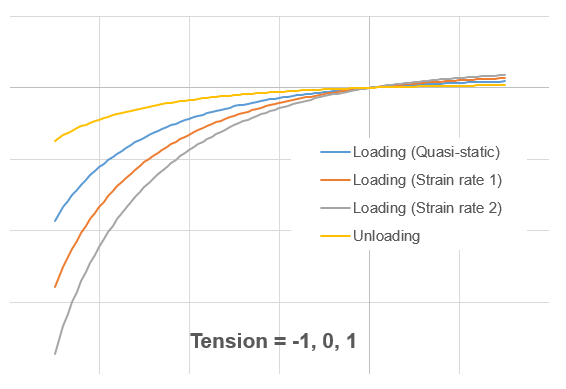
  Figure 1.
- Tension = -2
  
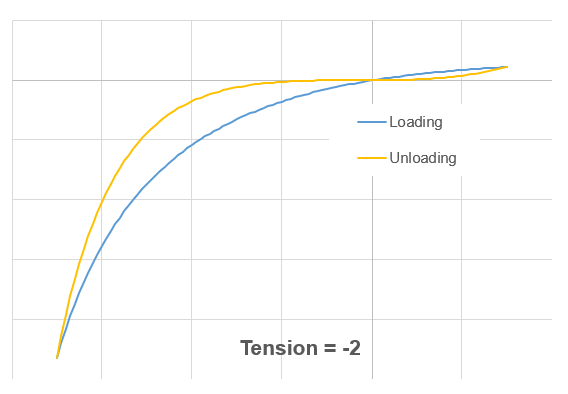
  Figure 2.
- Tension = other value
  
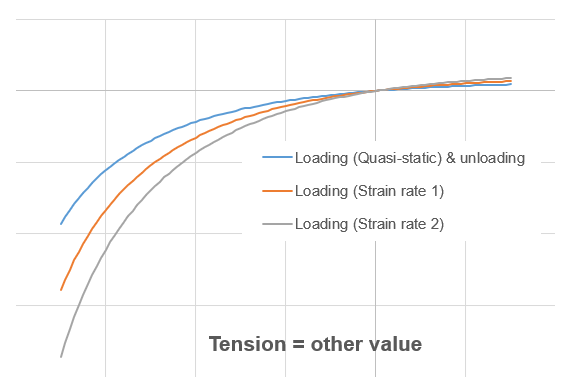
  Figure 3.
/VISC/PRONY can be used with this material law to include viscous effects.