/MAT/LAW33 (FOAM_PLAS)
Block Format Keyword This law models a viscous-elastic foam material with unloading/reloading like plastic behavior. This law is applicable only for solid elements and is typically used to model low density, closed cell polyurethane foams such as impact limiters.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW33/mat_ID/unit_ID or /MAT/FOAM_PLAS/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | Ka | fct_IDf | Fscalecrv | ||||||
| P0 | |||||||||
| A | B | C | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | Et | |||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Initial density. (Real) |
||
| E | Young's modulus. (Real) |
|
| Ka | Analysis type flag.
(Integer) |
|
| fct_IDf | Yield stress versus volumetric strain curve
function identifier. (Integer) |
|
| Fscalecrv | Scale factor for ordinate (stress) for
fct_IDf. Default = 1.0 (Real) |
|
| P0 | Initial air pressure. 5
(Real) |
|
| Ratio of foam to polymer
density. (Real) |
||
| Initial volumetric strain. (Real) |
||
| A | Yield parameter. (Real) |
|
| B | Yield parameter. (Real) |
|
| C | Yield parameter. (Real) |
|
| Tension stress cutoff (used only with
Ka
=2). Default = 120 (Real) |
||
| E1 | Coefficient for Young's modulus
update. (Real) |
|
| E2 | Coefficient for Young's modulus
update. (Real) |
|
| Et | Tangent modulus. (Real) |
|
| Viscosity coefficient in pure
compression. (Real) |
||
| Viscosity coefficient in pure
shear. (Real) |
Example (Foam)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/FOAM_PLAS/1/1
Foam
# RHO_I
2E-10
# E Ka func_IDf Fscalecurv
200 1 0 1
# P0 Phi Gamma_0
0 0 0
# A B C SIG_COFF
1E30 0 0 0
# E1 E2 Et eta_comp eta_shear
0 0 2 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- If the limiting yield curve is not
defined, then the material follows a
Maxwell-Kelvin-Voight visco-elastic model.
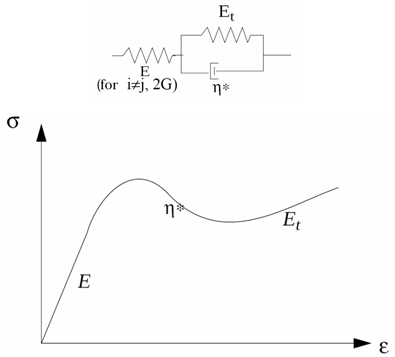
Figure 1. - If the limiting yield curve is defined, then the material initially follows the visco-elastic law until it intersects the defined yield curve, which limits the visco-elastic stress in tension and compression. The material does not experience plasticity, but instead behaves in a visco hyperelastic way.
- If the yield function
fct_IDf
= 0, then
(1) Where, is the volumetric strain:(2) - If the yield function
fct_IDf
≠ 0, then
versus
is read from input of the
curve identifier
fct_IDf.
The curve can be defined for tensile (
) and compression (
). The input stress
should be positive for both tension and
compression.
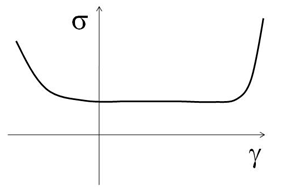
Figure 2. - The optional air pressure, as a
function of the volumetric strain can be added to
the structural pressure. Pressure is applied only
on the spherical part of the stress
tensor.
(3) - Young’s modulus is used as the initial
slope for unloading. It can be constant or
variable, based on the strain
rate.
(4) - The unloading or the loading direction
change (tensile <-> compression) is following
the current elastic modulus, like an isotropic
elastic-plastic material or highly viscous foam
material. However, there is no plastic strain
accumulation.
Figure 3.