Visco-elasto Materials for Foams (LAW33)
This material law can be used to model low density closed cell polyurethane foams, impactors, impact limiters. It can only be used with solid elements.
The main assumptions in this law are:
- The components of the stress tensor are uncoupled until full volumetric compaction is achieved (Poisson's ratio = 0.0).
- The material is isotropic.
- The effect of the enclosed air is considered via a separate Pressure versus Volumetric
Strain relation:
with:
Where,- Volumetric strain
- Porosity
- Initial air pressure
- Initial volumetric strain
- The structural stresses
follow the Maxwell-Kelvin-Voight viscoelastic model (Generalized Kelvin-Voigt Model (LAW35), Equation 12 before the limiting yield curve is
reached):
Figure 1. Maxwell-Kelvin-Voight Model 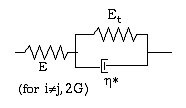
- The Young's modulus used in the calculation is:
- Yield is defined by a user-defined curve versus volumetric strain, , or
- Yield is applied to the principal structural stresses.
- Unloading follows Young's modulus, which results in viscous unloading.
- The full stress tensor is obtained by adding air pressure to the structual stresses: