/MAT/LAW38 (VISC_TAB)
Block Format Keyword This law describes the visco-elastic foam tabulated material and can only be used with solid elements.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW38/mat_ID/unit_ID or /MAT/VISC_TAB/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E0 | Iflag | Itota | |||||||
| H | RD | KR | KD | ||||||
| Kair | fct_IDp | FscaleP | |||||||
| P0 | RP | Pmax | |||||||
| fct_IDul | Fscaleunload | a | b | ||||||
| Nfunct | CUToff | Iinsta | |||||||
| Efinal | Visc | Tol | |||||||
| Fscale1 | Fscale2 | Fscale3 | Fscale4 | Fscale5 | |||||
| fct_ID1L | fct_ID2L | fct_ID3L | fct_ID4L | fct_ID5L | |||||
| fct_ID1ul | fct_ID2ul | fct_ID3ul | fct_ID4ul | fct_ID5ul | |||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| mat_title | Material title (Character, maximum 100 characters) |
|
| Initial density (Real) |
||
| E0 | Minimum tension modulus, used for
interface and time step computation. (Real) |
|
| Maximum Poisson's ratio in
tension. Default = 10-30 (Real) |
||
| Maximum Poisson's ratio in
compression. (Real) |
||
| Exponent for Poisson's ratio
computation. (Real) |
||
| Iflag | Analysis formulation type flag. 4
(Integer) |
|
| Itota | Incremental formulation flag.
(Integer) |
|
| Relaxation rate for unloading. Default = 10-30 (Real) |
||
| H | Hysteresis coefficient for
unloading. Default = 1.0 (Real) |
|
| RD | Damping factor on strain rate. Default = 0.5 (Real) |
|
| KR | Recovery model flag for unloading
(hysteresis loop).
Where, and are current internal energy and maximum internal energy, respectively. 6 (Integer) |
|
| KD | Decay model flag, hysteresis type.
(Integer) |
|
| Integration coefficient for
instantaneous module update. Default = 0.67 (Real) |
||
| Kair | Air content computation flag. 7
(Integer) |
|
| fct_IDp | Pressure curve identifier (pressure
versus relative volume). (Integer) |
|
| FscaleP | Pressure curve scale
factor. (Real) |
|
| P0 | Atmospheric
pressure. (Real) |
|
| RP | Relaxation rate of pressure. Default = 10-30 (Real) |
|
| Pmax | Maximum air pressure. Default = 1030 (Real) |
|
| Porosity (density of foam/density of
polymer). (Real) |
||
| fct_IDul | Unloading function identifier.
(Integer) |
|
| Fscaleunload | Unloading function scale
factor. Default = 1.0 (Real) |
|
| Unloading strain rate (must be greater
than
). (Real) |
||
| a | Exponent for stress
interpolation. Default = 1.0 (Real) |
|
| b | Exponent for stress
interpolation. Default = 1.0 (Real) |
|
| Nfunct | Number of functions defining rate
dependency (five or less). (Integer) |
|
| CUToff | Tension cutoff stress. The element is deleted when one element integration point exceeds the tension cutoff stress value. Default = 1030 (Real) |
|
| Iinsta | Material instability control flag.
(Integer) |
|
| Efinal | Maximum tension modulus. Default = E0 (Real) |
|
| Absolute value of strain at final
modulus. Default = 1.0 (Real) |
||
| Modulus interpolation
coefficient. Default = 1.0 (Real) |
||
| Visc | Maximum viscosity. 10 Default = 1030 (Real) |
|
| Tol | Tolerance on principal direction
update. Default = 1.0 (Real) |
|
| Fscalei | Scale factor for curve
i. (Real) |
|
| Engineering strain rate for curve
i. (Real) |
||
| fct_IDiL | Loading function identifier for curve
i. (Integer) |
|
| fct_IDiul | Unloading function identifier for curve
i. (Integer) |
Example (Foam)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/VISC_TAB/1/1
Foam
# RHO_I
2E-10
# E_0 nu_t nu_c R_V Iflag Itota
200 0 0 0 0 0
# Beta H R_D K_R K_D Teta
0 0 0 0 0 0
# K_air fct_ID_p Fscale_P
0 0 1
# P0 Rp Pmax Phi
0 0 0 0
#funID_unl Fscale_unload Eps_._unload a b
0 0 0 0 0
# N_funct CUT_off I_insta
1 0 0
# E_final Eps_final Lambda Visc Tol
0 0 0 0 0
# Fscale_i
1
# Eps_._i
0
# func_ID_iload
4
# func_ID_iunload
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/4
function_4
# X Y
-1 -200
1 200
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
Comments
- Engineering stress versus engineering strain can be input as functions for different strain rates. The stress and strain is positive in compression and negative in tension. By default (Itota=0), the tension behavior is linear elastic using Young’s modulus, E0. If Itota=1, the engineering stress strain behavior should be input using the functions, fct_IDiL, with the stress strain curve defined both in compression and tension
- When stress strain functions are
defined at different strain rates, the stresses are computed by interpolation from input
functions:
for given , read two values of function at for the two immediately lower and higher strain rates.
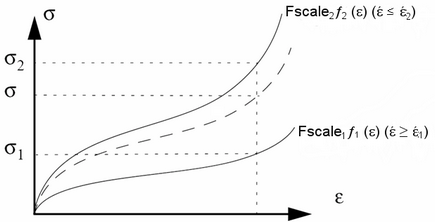
Figure 1. Two Strain Rate Curves (up to five may be input)with(1) The parameters and define the shape of the interpolation function within each interval. If = = 1, the interpolation is linear.
- A "coupled" set of principal
nominal stresses is computed with anisotropic Poisson's ratios:
in tension ( )
in compression.
Where, - Analysis formulation type Iflag.
Iflag=0: corresponds to the visco-elastic foam tabulated material (visco-elasticity is computed in each principal stress direction).
Iflag=1: behavior will be linear in both tension and compression, following Hook's relations.
For compression, Young's modulus and Poisson's ratio are used.
In tension, the instantaneous Young's modulus ratio is used.
The instantaneous Young’s modulus is updated using:(2) with(3) Where,- Minimum tension modulus
- Maximum tension modulus
- Relative volume computed in Radioss
- Absolute value of the strain corresponding to the maximum compression modulus.
The instantaneous modulus is only used for tension.
- For stability,
is filtered using:
(4) - Hysteresis is applied in linear
tension case.
If KR=1, Hysteresis is only applied in compression.
If KR=2, Hysteresis is applied both in compression and in tension.
- For air pressure
(when
Kair=1)If fct_IDp≠0:
(5) Where, refers to function number fct_IDp.
If fct_IDp=0:(6) Relaxation is applied as:(7) Where, is the relaxation rate of pressure and t is the time.
- During unloading, without an
unloading curve defined fct_IDiul =
fct_IDul=0,
is computed from the first loading curve,
fct_ID1L.
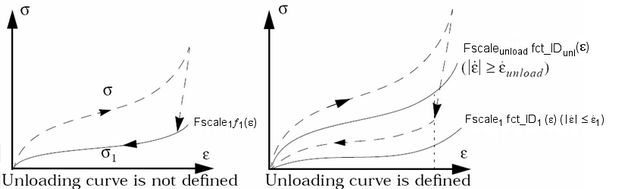
Figure 2.If the unloading curve is defined, is interpolated between the first loading curve fct_ID1L and the defined unloading curve fct_IDul or fct_IDiul. In this case, fct_ID1L must correspond to a quasi-static state.
- Unloading functions fct_IDiul (Line 12) are used only if the unloading curve fct_IDul is not defined.
- If Visc
is input, interpolated stress will be limited by this value to have a larger
timestep:
(8) - The behavior is strain rate independent when .
- /VISC/PRONY can be used with this material law to include viscous effects.