Nonlinear Fatigue Analysis

An overview of the different methods available for both SN and EN Fatigue analyses is provided. PARAM,NLFAT,YES is required to turn ON Fatigue analysis using Nonlinear Static Analysis results.

SN Fatigue Analysis

When SN fatigue analysis is carried out with nonlinear analysis results, fatigue damage is calculated in 3 different scenarios.

Nonlinear Analysis without Cyclic Load History in Fatigue Analysis
If a TABFAT entry is not assigned to FATLOAD entry for Nonlinear Static Analysis based Fatigue analysis, then all incremental stresses are used in Fatigue analysis as if the stress at each load increment were stress at each time step. These incremental stresses are then used for Rainflow counting and subsequent damage calculations.
Figure 1. SN Fatigue – Without TABFAT Cyclic Load History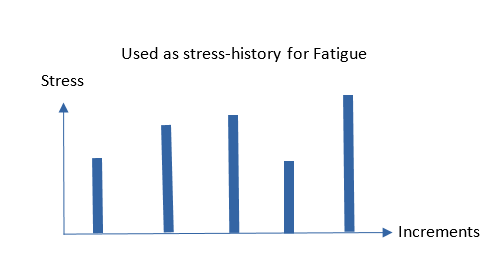
Nonlinear Analysis with Cyclic Load History in Fatigue Analysis
If a TABFAT entry is assigned to FATLOAD entry for Nonlinear Static Analysis based Fatigue analysis, then the stress history is obtained from the load history of the TABFAT applied to stress at the last step of the nonlinear analysis. The load history is then used for Rainflow counting and subsequent damage calculations.
Figure 2. SN Fatigue – With TABFAT Cyclic Load History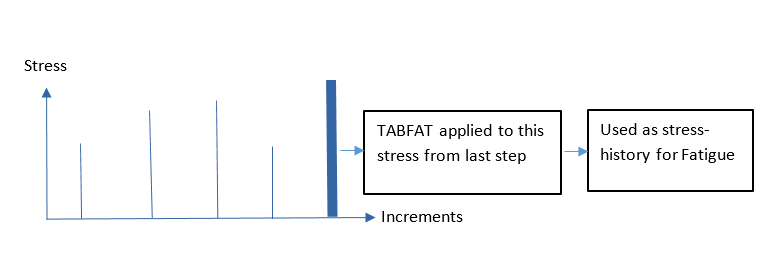
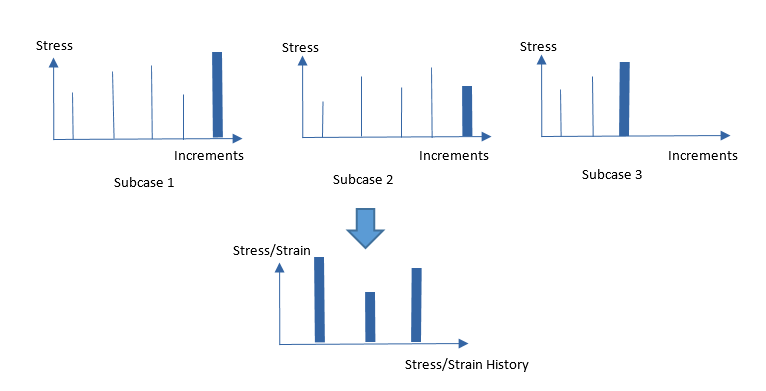
Nonlinear Analysis with SQNTL specified on FATEVNT for Fatigue Analysis
If SQNTL is specified on the FATEVNT entry, then stress at the last step of each subcase is used to form a stress history. The number of increments does not need to be consistent across the different nonlinear subcases. This stress history is then used for Rainflow counting and subsequent damage calculations.
Figure 3. SN Fatigue – With SQNTL on FATEVNT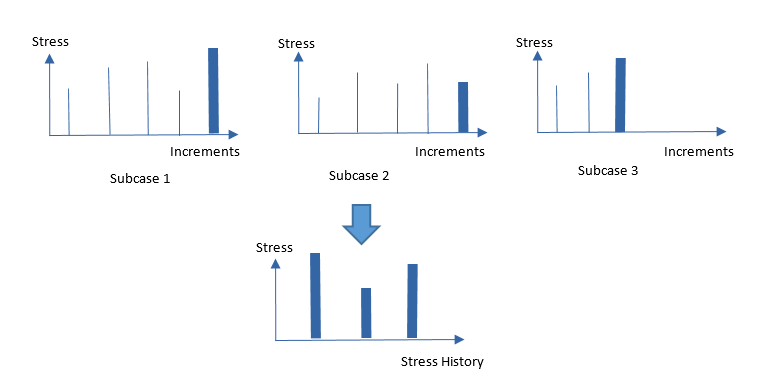

EN Fatigue Analysis

When EN fatigue analysis is carried out with nonlinear analysis results, cyclic strength coefficient (K’) and cyclic strain hardening exponent (n’) are not required. No plasticity correction such as Neuber correction, Hoffmann-Seeger correction, and Jiang-Sehitoglu plasticity model is involved in damage calculation as stresses and strains are already elasto-plastic stresses and strains. A basic assumption in fatigue analysis with nonlinear analysis results is that stress and strain coming from nonlinear analysis describes cyclic behavior of the material in use.

Since linear superposition of stress and strain is invalid in nonlinear analysis, only one FATLOAD is allowed in a FATEVNT entry, unless SQNTL is specified.

The following three different scenarios are available for calculating EN damage with nonlinear analysis results.

Nonlinear Analysis without Cyclic Load History in Fatigue Analysis
If a TABFAT entry is not assigned to FATLOAD entry for Nonlinear Static Analysis based Fatigue analysis, then all incremental stresses and strains are used as if they were stresses and strains at each time step. In uniaxial fatigue, combined stress and strain are calculated using user-defined combination method. In multiaxial fatigue, the stresses and strains are directly fed to multiaxial fatigue calculations without going through Jiang-Sehitoglu plasticity models.
Figure 4. EN Fatigue – Without TABFAT Cyclic Load History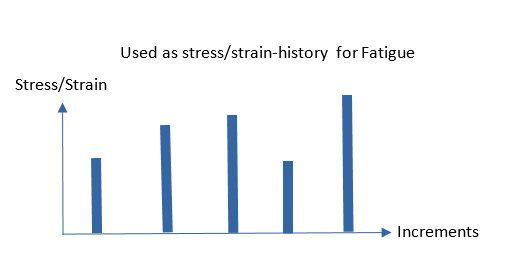
Nonlinear Analysis with Cyclic Load History in Fatigue Analysis and Monotonic load in nonlinear analysis
If a TABFAT entry is assigned to FATLOAD entry for Nonlinear Static Analysis based Fatigue analysis, then a monotonic load is assumed for nonlinear analysis, and principal stress-principal strain relationship in an element/a grid of interest is calculated (Figure 5). The purpose of nonlinear analysis with monotonic load is to obtain material information required for EN fatigue analysis. The principal stress-principal strain relationship is considered as the cyclic stress-strain curve (Figure 6).
Figure 5. EN Fatigue – Stress/Strain versus Load Factor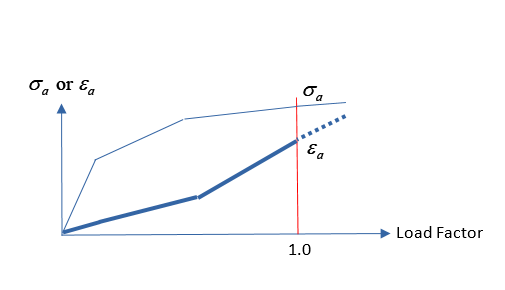

Figure 6. EN Fatigue – Cyclic Stress-Strain Curve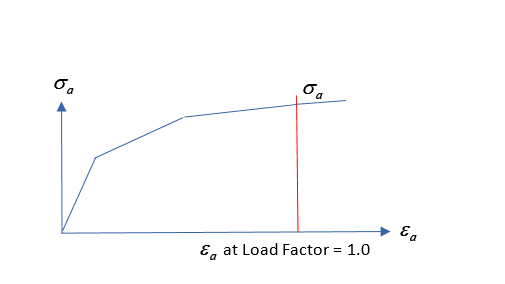

Rainflow counting is then performed on load-time history of the TABFAT entry assigned to the FATLOAD entry. Change of stress and strain ( $Δ σ$ and $Δ ε$ ) with respect to change of load ( $Δ l o a d$ ) in load-time history can be computed using the cyclic stress-strain curve as:
$\frac{Δ l o a d}{2} \to \frac{Δ ε}{2} \to \frac{Δ σ}{2}$
By accumulating change of the stress and strain, you can find the complete stress history and strain history with respect to the load history. This process is as good as the combination of Ramberg-Osgood equation and Neuber correction in damage calculation with linear analysis results.
The Rainflow cycle counting starts from the maximum absolute valley or peak of the load. The stress-strain relationship is only valid until load factor becomes 1.0. Thus the initial loading which is the absolute maximum valley or peak is not supposed to be greater than 1.0. This implies that the absolute maximum value of the load history should be ideally less than or equal to 1.0 after the scale and offset are applied. If the absolute maximum value of the load history is greater than 1.0, extrapolated stress and strain are used for an initial loading point as depicted (Figure 6). Likewise, extrapolated $\frac{Δ ε}{2}$ and $\frac{Δ σ}{2}$ are used for change of stress and strain if $\frac{Δ l o a d}{2}$ is greater than 1.0.
Damage is calculated via biaxial fatigue analysis. Therefore you need to choose multiaxial fatigue analysis option in FATPARM, and otherwise, the run will error out.
Nonlinear Analysis with SQNTL specified on FATEVNT for Fatigue Analysis
If SQNTL is specified on the FATEVNT entry, then stress at the last step of each subcase is used to form a stress history and a strain history. The number of increments does not need to be consistent across the different nonlinear subcases.
Figure 7. EN Fatigue – With SQNTL on FATEVNT