Matériau doux isotrope : hystérésis par modèle de Jiles-Atherton
Introduction
Dans Flux, les matériaux décrit par modèle de Jiles-Atherton permettent de prendre en compte les phénomènes d'hystérésis pendant la résolution du projet, comme les modèles de Preisach. Cela permet d'avoir une meilleure précision, notamment pour le calcul des pertes fer, qui peuvent être évaluées par un calcul direct, c'est-à-dire par une approche de type à priori. Les applications typiques des modèles d'hystérésis sont les actionneurs linéaires, les actionneurs avec entrefers petits, les dispositifs avec tores etc.
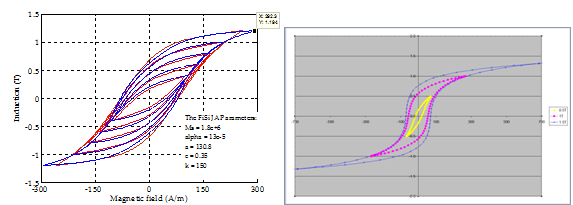
Modèle d'hystérésis Jiles-Atherton dans Flux
Il s'agit d'un modèle de matériaux hystérétique isotrope, vectoriel et statique de Jiles-Atherton (J-A).
Il est défini par les cinq paramètres rentrés par l'utilisateur, présentés dans le tableau ci-dessous.
Il est accessible en application Magnétique Transitoire en 2D et 3D.
| Paramètre | Propriété physique |
|---|---|
| Msat | Aimantation à saturation |
| a | Facteur de forme pour l'aimantation anhystérétique |
| k | Coefficient d'accrochage des parois |
| c | Coefficient lié aux mouvements réversibles des parois |
| α | Paramètre de champ moyen représentant le couplage entre domaines |
Tableau 1. Les cinq paramètres du modèle de Jiles-Atherton
Avantages et inconvénients du modèle J-A
L'avantage du modèle vectoriel par rapport au modèle scalaire, est qu'il permet d'étudier des applications avec champ tournant.
L'avantage du modèle J-A est qu'il est défini par uniquement cinq paramètres, et en plus il s'agit de paramètres physiques du matériau (contrairement au modèle Preisach, fondé sur la description mathématique).
D'autre part, le modèle J-A présente parfois des problèmes de convergence et la modélisation des cycles mineurs est moins précise qu'avec les modèles de Preisach.
Références
Le modèle implémenté dans Flux a été établi par Johan Gyselinck et Ruth V. Sabariego. Pour plus d'informations techniques sur le modèle, consulter leurs deux articles :
- J. Gyselinck, P. Dular, N. Sadowski, J. Leite and J.P.A. Bastos, “Incorporation of a Jiles-Atherton vector hysteresis model in 2D FE magnetic field computations – Application of the Newton-Raphson method”, COMPEL, vol. 23, no. 3, pp. 685–693, 2004.
- J. Gyselinck, L. Vandevelde, J. Melkebeek and P. Dular, “Complementary two-dimensional finite element formulations with inclusion of a vectorized Jiles-Atherton model”, COMPEL, vol. 23, no. 4, pp. 959–967, 2004.