Évaluation à priori des pertes fer dans les noyaux magnétiques

Introduction

Cette page traite du calcul des pertes fer dans les noyaux magnétiques dont le matériau est défini dans un projet Flux par un des modèles de Preisach :

Hystérétique isotrope, modèle de Preisach décrit par 4 paramètres d'un cycle typique et
Hystérétique isotrope, modèle de Preisach identifié par N triplets

ou par celui de Jiles-Atherton :

Hystérétique isotrope, modèle de Jiles-Atherton

Les matériaux possédant ces types de propriété B(H) prennent en compte les phénomènes d'hystérésis ferromagnétique pendant la résolution du projet et par conséquent, ils permettent une évaluation directe ou à priori des pertes hystérétiques et des pertes fer dans les matériaux ferromagnétiques.

Les sujets suivants sont traités dans les prochaines sections :

Hystérésis statique et dynamique
Évaluation des pertes hystérétiques et des pertes fer dans Flux pour un matériau hystérétique
Exemple d'application
Références bibliographiques

Hystérésis statique et dynamique

Durant leur fonctionnement, plusieurs parties des appareils électromécaniques sont soumises à des variations temporelles de champ magnétique, qui génèrent - dans les volumes des matériaux ferromagnétiques caractérisés par un comportement hystérétique - ce qui est appelé pertes hystérétiques : en effet, pendant les processus de démagnétisation le matériau ne restitue pas entièrement l'énergie accumulée durant les phases de magnétisation, mais il dissipe une partie de cette énergie sous forme de chaleur.

De plus, les variations de champ magnétique induisent - dans les volumes conducteurs - des courants (appelés aussi courants de Foucault) qui se traduisent en pertes via l’effet Joule. Ces deux contributions forment ce que l’on appelle plus communément les pertes fer qui sont identifiées via l’expression générale suivante :

$dP = H . \frac{\partial B}{\partial t} + ρ J^{2}$ (1)

où :

dP : la densité de pertes fer (W/m³) ;
H : le champ magnétique (A/m) ;
B : l'induction magnétique (T) ;
ρ : la résistivité électrique du matériau (Ω.m) ;
J : la densité de courant induite (A/m²).

Dans (1), les deux contributions mentionnées ci-dessus peuvent être clairement distinguées. Dans le cas d'un champ magnétique à variation temporelle lente, le terme de pertes Joule $ρ J^{2}$ est petit car les courants induits sont négligeables et les pertes sont presque purement de nature hystérétique. D'autre part, lorsque la variation temporelle des champs augmente (c.-à-d., la fréquence augmente), les pertes hystérétiques et les pertes Joule ont tendance à augmenter.

Pour représenter graphiquement ce comportement, une autre expression - similaire à (1) - pour la densité de pertes fer dP peut être dérivée en utilisant des grandeurs macroscopiques mesurables (plus de détails dans les références bibliographiques à la fin de cette page) :

$dP = Hs . \frac{\partial Ba}{\partial t}$ (2)

où :

dP est la densité de pertes fer dans la région (W/m³) ;
Hs est le champ magnétique surfacique sur la région (A/m) et
Ba est l'induction magnétique moyenne dans la section de la région (T).

Le seul terme à second membre de cette équation (2) tient compte à la fois des pertes hystérétiques et des pertes par courants de Foucault, parce que Hs et Ba sont des fonctions de la distribution globale des champs dans la région (y compris la contribution provenant des courants de Foucault à des fréquences plus élevées) et donc le terme $Hs . \frac{\partial Ba}{\partial t}$ représente la totalité des pertes fer dans la région et pas seulement les pertes hystérétiques.

Il résulte de ce qui précède que l'aire décrite par le cycle d'hystérésis de Ba(Hs) (voir l'image ci-dessous) représente l'énergie totale dissipée durant un cycle (c'est-à-dire la somme des contributions par hystérésis et par effet Joule) :

aux basses fréquences, le cycle d'hystérésis est étroit en raison des courants induits et des pertes Joule négligeables : ces conditions sont généralement désignées comme hystérésis statique ;
aux fréquences plus élevées, le cycle d'hystérésis Ba(Hs) s'élargit du fait du développement de courants induits conduisant à des pertes Joule : ces situations sont identifiées comme hystérésis dynamique.

Figure 1. Cycle d'hystérésis statique pour une fréquence de 10 Hz (en rouge) et cycle d'hystérésis dynamique pour une fréquence de 1000 Hz (en bleu) dans une région magnétique avec courants induits.

Prise en compte des pertes hystérétiques et des pertes fer dans Flux pour un matériau hystérétique

Dans un projet Flux avec application Magnétique Transitoire, l'utilisateur peut choisir entre deux approches pour calculer les pertes fer pendant la résolution :

Représenter uniquement l’hystérésis statique : un matériau avec une propriété B(H) hystérétique basée le modèle de Preisach ou de Jiles-Atherton doit être défini et assigné à une région magnétique non-conductrice. Cette approche est bien adaptée pour les problèmes à basse fréquence.
Inclure l’hystérésis dynamique, c'est-à-dire évaluer l'augmentation des pertes fer dues aux courants induits: le matériau contenant une propriété B(H) de type Preisach ou Jiles-Atherton doit aussi avoir une propriété J(E) et être assigné à une région de type conducteur massif et non pas à une région magnétique non-conductrice.

Dans le premier cas (c'est-à-dire hystérésis statique : matériau avec propriété B(H) et région magnétique non-conductrice), Flux fournit à l’utilisateur la quantité dPowMagV :

qui est disponible dans l'éditeur de formules à travers le bouton dPuissMag / dV à utiliser en post-traitement pour l'affichage graphique (par exemple les isovaleurs) de la densité de puissance magnétique (c'est-à-dire la densité des pertes hystérétiques) ;
et qui peut être intégrée sur les volumes des régions à travers un Capteur pour obtenir la puissance totale dissipée par l'hystérésis statique (c'est-à-dire les pertes hystérétiques) :

A ce but l'utilisateur doit :

créer un Capteur par le menu Paramètre/Grandeur ou Calcul selon que le projet soit respectivement non-résolu ou résolu ;
choisir Prédéfini comme type de capteur ;
et Puissance magnétique comme quantité à calculer ;
sélectionner les régions de type magnétique non-conductrice ayant une propriété B(H) hystérétique ;
évaluer le capteur.

Dans le deuxième cas (c'est-à-dire hystérésis dynamique : matériau ayant des propriétés B(H) et J(E) et région de type conducteur massif), Flux fournit à l’utilisateur la quantité dPowV :

qui est disponible dans l'éditeur de formules à travers le bouton dPuissance / dV à utiliser en post-traitement pour l'affichage graphique (par exemple les isovaleurs) de la densité de puissance totale (c'est-à-dire la densité des pertes fer) ;
et qui peut être intégrée sur les volumes des régions à travers un Capteur pour obtenir la puissance globale dissipée par l'hystérésis dynamique (c'est-à-dire les pertes fer) :

A ce but l'utilisateur doit :

créer un Capteur par le menu Paramètre/Grandeur ou Calcul selon que le projet soit respectivement non-résolu ou résolu ;
choisir Intégrale comme type de capteur ;
sélectionner les régions de type conducteur massif ayant une propriété B(H) hystérétique et un modèle de conductivité J(E) ;
dans le champ Formule spatiale, sélectionner la quantité dPuissance / dV dans l'éditeur de formule ;
évaluer le capteur.

Le tableau ci-dessous résume les deux possibilités de modélisation évoquées précédemment pour calculer soit les pertes hystérétiques avec de l'hystérésis statique soit les pertes fer avec de l'hystérésis dynamique.

Tableau 1. Récapitulatif du calcul des pertes hystérétiques et des pertes fer pour un modèle hystérétique.
Matériau	Propriété active	Région	Méthode de calcul	Grandeur calculée
Matériau doux isotrope : hystérésis par modèles de Preisach ou Matériau doux isotrope : hystérésis par modèle de Jiles-Atherton	B(H)	Magnétique non conductrice	Capteur prédéfini (type puissance magnétique) sur région (quantité dPuissMag / dV)	Pertes hystérétiques
	B(H) et J(E)	Conducteur massif	Capteur intégrale de la grandeur dPuissance / dV sur région	Pertes fer

Exemple d'application

Considérons à nouveau le problème TEAM 32 déjà présenté dans cette page et utilisons-le pour comparer le calcul des pertes fer avec les deux approches vus précédemment, à savoir :

la modélisation de l'hystérésis statique : basée sur un matériau avec une propriété B(H) de type Preisach assigné à une région magnétique non conductrice ;
la modélisation de l'hystérésis dynamique : basée sur un matériau ayant une propriété B(H) de type Preisach et une propriété J(E) linéaire isotrope assigné à une région de type conducteur massif.

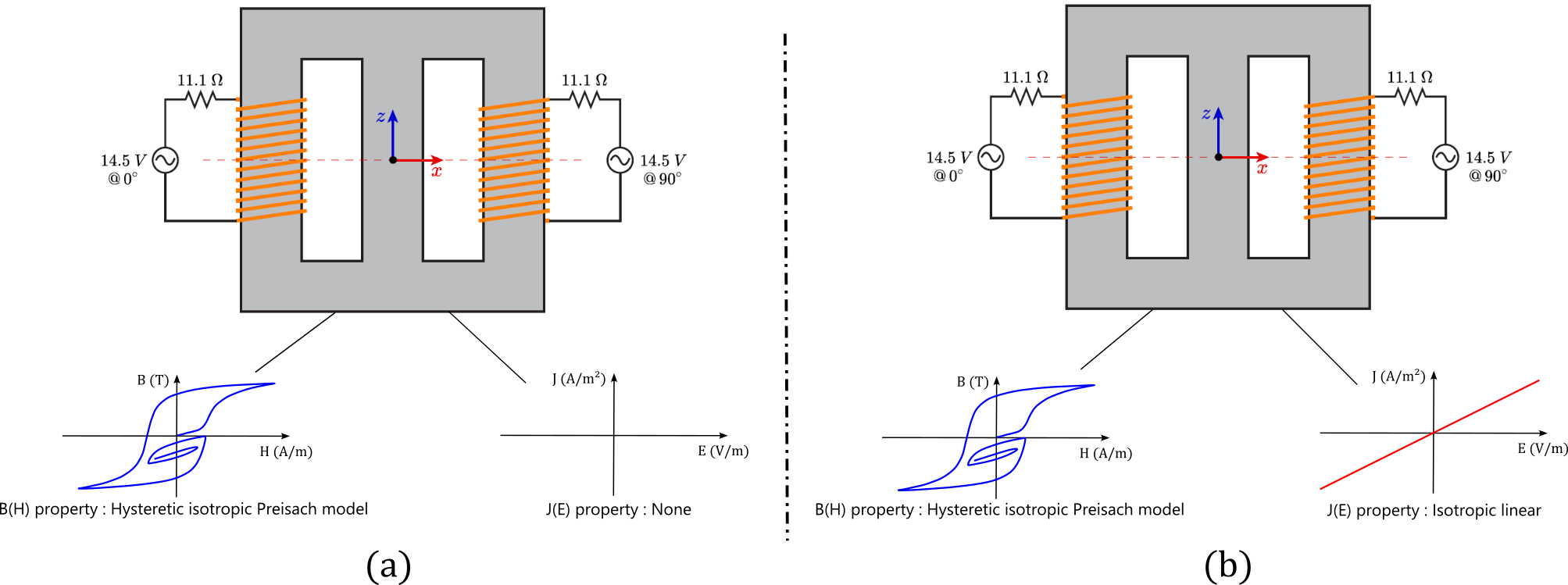
L'application de ces deux approches au problème TEAM 32 est synthétisée dans la figure ci-dessous :

Figure 2. Représentation 2D du problème TEAM 32 avec a) l'approche avec une région magnétique non conductrice et une propriété B(H) hystérétique et b) l'approche avec une région de type conducteur massif, une propriété B(H) hystérétique et une propriété J(E) linéaire isotrope.

Les deux sources de tension qui alimentent le circuit imposent une tension sinusoïdale avec une amplitude de 14.5 V et un déphasage de 90° entre elles. Plusieurs simulations sont réalisées, sur une plage de fréquence pour les sources de tension allant de 1 à 100 Hz avec les deux approches. Le but est de comparer les pertes hystérétiques avec les pertes fer globales à chaque fréquence.

Après résolution, une comparaison entre les deux approches précédente peut donc être faite en comparant les pertes fer globales avec les pertes hystérétiques, comme montré dans la figure ci-dessous :

Figure 3. Puissance totale dissipée dans le noyau magnétique en fonction de la fréquence d'alimentation. En orange l'approche avec une région magnétique non conductrice et une propriété B(H) hystérétique ; en bleu l'approche avec une région de type conducteur massif, une propriété B(H) hystérétique et une propriété J(E) linéaire isotrope.

La répartition des courants induits peut être visualisée à l'aide des flèches de la densité de courant J dans le noyau magnétique, comme montré dans la figure ci-dessous.

Figure 4. Répartition des courants induits qui évoluent dans le volume du noyau magnétique calculés avec l'approche basée sur une région de type conducteur massif, une propriété B(H) hystérétique et une propriété J(E) linéaire isotrope.

Références bibliographiques

H. Pfützner and G. Shilyashki, "Theoretical Basis for Physically Correct Measurement and Interpretation of Magnetic Energy Losses," in IEEE Transactions on Magnetics, vol. 54, no. 4, pp. 1-7, April 2018, Art no. 6300207, doi: 10.1109/TMAG.2017.2782218.
M. Tousignant. Modélisation de l’hystérésis et des courants de Foucault dans les circuits magnétiques par la méthode des éléments finis. Energie électrique. Université Grenoble Alpes; Polytechnique Montréal (Québec, Canada), 2019. (in French). ⟨NNT : 2019GREAT065⟩. ⟨tel-02905410⟩