Since version 2026, Flux 3D and Flux PEEC are no longer available.

Please use SimLab to create a new 3D project or to import an existing Flux 3D project.

Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).

/!\ Documentation updates are in progress – some mentions of 3D may still appear.

Magnet (vector): linear approximation

Presentation

These models ( Linear magnet described by the Cartesian / cylindrical / spherical vector Br ) define a B(H) dependence of linear demagnetization in Flux (not available in material manager).

Main characteristics:

  • the mathematical model and the direction of magnetization are associated
  • same number of materials and/or coordinate systems than regions

Mathematical model

In the direction of magnetization the model is a straight line.

The corresponding mathematical formula is written as follows:

Β(Η)=μ0μrΗ+ Br

where:

  • μ0 is the permeability of vacuum, μ0 = 4 π 10-7 H/m
  • μr is the relative permeability (recoil line slope)
  • Br is the remanent flux density (T)

The shape of the B(H) dependence is given in the opposite figure:

Direction of magnetization

The direction of magnetization is “associated” with the model. Three models are provided: Cartesian, cylindrical or spherical vector.

Cartesian magnetization

The mathematical model is the linear model previously described.

The B(H) dependence is defined by the following relationship in a Cartesian coordinate system:

where:

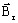  • is the remanent flux density defined by three components following the three axes of the Cartesian coordinate system: ( Brx, Bry, Brz)
  • μr is the tensor of relative permeability; the three numerical values ( μrx, μry, μrz) correspond to the three axes of the Cartesian coordinate system

Cylindrical magnetization

The mathematical model is the linear model previously described.

The B(H) dependence is defined by the following relationship in a cylindrical coordinate system:

where:

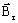  • is the remanent flux density defined by three components following the three axes of the cylindrical coordinate system: ( Brr, Brθ and Brz)
  • μ r is the relative permeability
radial (Brr ) orthoradial (Brθ) axial (Brz)

Spherical magnetization

The mathematical model is the linear model previously described.

The B(H) dependence is defined by the following relationship in a spherical coordinate system:

where:

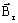  • is the remanent flux density defined by three components following the three axes of the spherical coordinate system: ( Brr, Brθ et Brφ)
  • μ r is the relative permeability

radial (Brr ):