tsp
Traveling salesman problem.
Attention: Valid only with Altair Advanced Optimization
Extension
Syntax
[SeqCus,totalCost] = tsp(D)
[SeqCus,totalCost] = tsp(D, options)
Inputs
- D
- A distance matrix such that D(i,j) is the distance from customer i to customer j.
- options
- A struct containing the genetic algorithm option settings.
Outputs
- SeqCus
- The customer indices for the solution path.
- totalCost
- The total path distance, including a return to the start.
Examples
Find a short path through the following customer locations map.
% create customer site list, transposing locations from columns to rows
sites = [77, -60, -86, 24, 46, -9, 9, 2, 42, -31, -77, -24, 60, 31, 86, -2, -42, -46;
59, 55, -27, -10, -88, 70, -70, 9, -2, -48, -59, 10, -55, 48, 27, -9, 2, 88].';
% create distance matrix
n = size(sites, 1);
D = zeros(n);
for ii = 1:n
s1 = sites(ii,:);
for jj = ii:n
s2 = sites(jj,:);
D(ii,jj) = norm(s2-s1);
D(jj,ii) = D(ii,jj);
end
end
% find solution
options = gaoptimset('Seed', 2023);
[SeqCus,totalCost] = tsp(D, options)
% plot solution path
optPath = sites(SeqCus',:);
optPath(n+1,:) = optPath(1,:);
scatter(sites(:,1), sites(:,2), 'ob', 'markersize', 4);
hold on;
plot(optPath(:,1), optPath(:,2));
legend('Sites', 'Path');SeqCus = [Matrix] 1 x 18
16 8 12 2 18 6 14 1 15 9 4 13 5 7 10 11 3 17
totalCost = 732.656301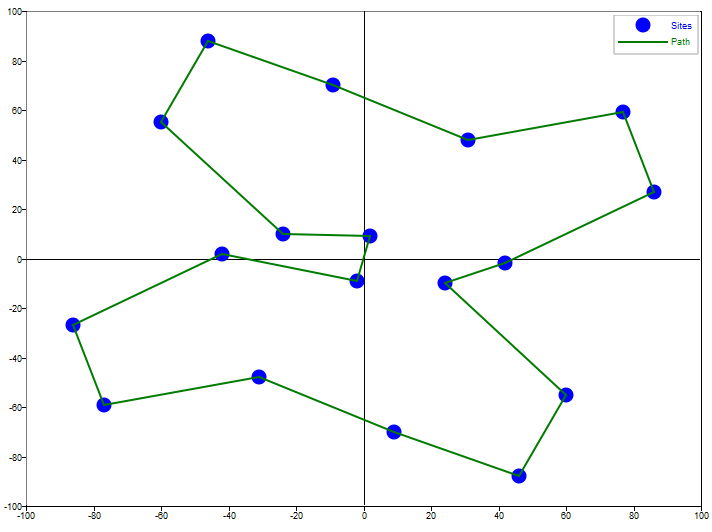
The function is implemented as a genetic algorithm. The gaoptimset options and defaults are as follows:
- Generations: 100
- PopulationSize: 6
- Seed: 0
Larger numbers of generations and population size allow the search to proceed longer.
A non-zero seed will make the result repeatable.