/INTER/TYPE11

Format

Definition

Flags for Deactivation of Boundary Conditions: IBC

Definition

Comments

1. A non-zero Gap_min value must be input in case of a line is a spring element.
2. In case of SPMD, each main segment defined by line_ID_m must be associated to an element (possibly to a void element).
3. The secondary and main lines are defined using Lines option. A self-impacting contact is defined when line_ID_s > 0 and line_ID_m = 0.
4. Flag I_del =1 has a CPU cost higher than I_del =2.
5. A default value for Gap_min is computed as:
   $$\mathit{Ga}{p}_{\min }=g_{m\_\min }+g_{s\_\min }$$
   While,

   $g_{m\_\min }=\min \left(\frac{t}{2},\frac{l}{20},\frac{\sqrt{S}}{2}\right)$

   Main surface gap

   $t$

   Average thickness of the main elements for shell elements

   $l$

   Length of the smallest side of solid elements

   $S$

   Smallest cross section of the beam and truss elements

   $g_{s\_\min }$

   Secondary surface gap: computation identical to $g_{m\_\min }$ ; except that it is applied on secondary side elements.

6. Variable gap
   • If I_gap = 1000, gap is constant and is equal to Gap_min.
   • If I_gap = 1, gap is variable and is computed for each impact as:
     $$g_m+g_s$$
   • If I_gap = 3, gap is variable and is computed for each impact as:
     $$\max \left\{Ga{p}_{\min },\min \left[\left(g_s+g_m\right),\%mesh\_size\cdot \left(g_{s\_l}+g_{m\_l}\right)\right]\right\}$$
     Where,

     $g_m$

     Main element gap

     $g_m=\frac{t}{2}$

     With $t$ thickness of the main element for shell elements

     $g_m=\frac{l}{10}$

     With $l$ length of the smallest side of a solid element

     $g_m=\frac{\sqrt{S}}{2}$

     With $S$ being the cross section of the truss and beam elements

     $g_m=0$

     For spring elements

     $g_s$

     Is computed the same way; except that it is applied on secondary side elements

     $g_{m\_l}$

     Length of the smaller edge of element

     $g_{s\_l}$

     Length of the smaller edge of elements connected to the secondary node

     The variable gap is always at least equal to Gap_min.

7. Contact stiffness

   There is no limitation value on the stiffness factor (but a value greater than 1.0 can reduce the initial time step). Contact stiffness for shell, solid and beam elements is computed as:

   If I_stf =1:

   $$K=Stfac$$

   If I_stf = 2, 3, 4 or 5:

   $$K=\text{max}\left[S{t}_{\text{min}},\text{min}\left(S{t}_{\text{max}},K_n\right)\right]$$
   Where,

   • $K_n$ is computed from both main segment stiffness $K_m$ and secondary segment stiffness $K_s$ as follows, if I_stf ≠ 1:

     I_stf = 2, $K_n=\frac{K_m+K_s}{2}$

     I_stf = 3, $K_n=\max \left(K_m,K_s\right)$

     I_stf = 4, $K_n=\min \left(K_m,K_s\right)$

     I_stf = 5, $K_n=\frac{K_m\cdot K_s}{K_m+K_s}$

   • Where, $K_m$ is main segment stiffness and computed as:

     when main segment lies on a shell or is shared by shell and solid:

     $$K_m=Stfac\cdot 0.5\cdot E\cdot t$$

     when main segment lies on a solid:

     $$K_m=Stfac\cdot B\cdot \frac{S^2}{V}$$
     Where,

     $S$

     Segment area

     $V$

     Volume of the solid

     $B$

     Bulk modulus

   • $K_s$ is an equivalent nodal stiffness considered:

     when node is connected to a shell element:

     $$K_s=\frac{1}{2}\cdot E\cdot t$$

     when node is connected to solid element:

     $$K_s=B\cdot \sqrt[3]{V}$$

   When using /PROP/VOID and /MAT/VOID, material properties and thickness for the VOID material must be entered otherwise the contact stiffness of the void elements will be zero. This is especially important if VOID shell elements share elements with solid elements as the stiffness of the shell elements is used in the contact calculation.

   For spring elements not attached to any other elements, use I_stf=1 and specify the contact stiffness using Stfac. Otherwise, no contact will be detected.

8. Deactivation of boundary condition is applied to nodes of surface 1.
9. Inacti = 3 may create initial energy if the node belongs to a spring element.
   Inacti = 6 is recommended instead of Inacti = 5, to avoid high frequency effects into the interface.

   
   
   

10. The sorting factor Bumult is used to speed up the sorting algorithm.
11. The default value for Bumult is automatically increased to 0.30 for models which have more than 1.5 million nodes and to 0.40 for models with more than 2.5 million of nodes.
12. If the time step of a secondary node in this contact becomes less than dtmin, the secondary node is deleted from the contact and a warning message is printed in the output file. This dtmin value takes precedence over any model interface minimum time step entered in /DT/INTER/DEL.
13. When sens_ID is defined for activation/deactivation of the interface, T_start and T_stop are not taken into account.
14. If fric_ID is defined, the contact friction is defined in /FRICTION and the friction input Fric in this input card is not used.

    For friction formulation:

    Friction penalty formulation I_form

    • If I_form = 1, (default) viscous formulation, the friction forces are:
      $$F_t=\min \left(\mu F_n,F_{adh}\right)$$

      While an adhesion force is computed as:

      $F_{adh}=C\cdot V_t$ with $C=VI{S}_F\cdot \sqrt{2Km}$

    • If I_form = 2, stiffness formulation, the friction forces are:
      $$F_t^{new}=\min \left(\mu F_n,F_{adh}\right)$$

      While an adhesion force is computed as:

      $F_{adh}=F_t^{old}+\text{Δ}{F}_t$ with $\text{Δ}{F}_t=K\cdot V_t\cdot dt$

      Where, $V_t$ is tangential velocity of the secondary node relative to the main segment.

      I_form = 2 is recommended for implicit and low speed impact explicit analysis.

15. Heat exchange:
    By I_the=1 (heat transfer activated) to consider heat exchange and heat friction in contact.

    • If I_the = 0, then heat exchange is between shell and constant temperature contact T_int.
    • If I_{the_form} = 1, then heat exchange is between all contact pieces.

    T_int is used only when I_{the_form}=0. In this case. The temperature of main side assumed to be constant (equal to T_int). If I_{the_form}=1 then T_int is not taken into account. So, the nodal temperature of main side will be considered.

    If I_the > 1, the material of the secondary side needs to be a thermal material using finite element formulation for heat transfer (/HEAT/MAT).

    Heat exchange coefficient:

    • If fct_ID_K = 0, then K_the is heat exchange coefficient, and the heat exchange depends only on heat exchange surface.
    • If fct_ID_K ≠ 0, K_the is a scale factor, and the heat exchange depends on contact pressure:
    $$\mathrm{K}=K_{the}\cdot {\mathrm{f}}_K\left(Ascal{e}_K,P\right)$$

    While, $f_K$ is the function of fct_ID_K.

16. Thermal conduction is computed when the secondary node falls into the Gap.
17. Radiation is considered in contact if $F_{rad}\ne 0$ and the distance, $d$ , of the secondary node to the main segment is:
    $$Gap<d<D_{rad}$$
    While $D_{rad}$ is the maximum distance for radiation computation. The default value for $D_{rad}$ is computed as the maximum of:

    • Upper value of the Gap (at time 0) among all nodes
    • Smallest side length of secondary element

    It is not recommended to set the value too high for $D_{rad}$ , which may reduce the performance of Radioss Engine. The heat exchange is computed only from main to secondary.

    A radiant heat transfer conductance is computed as:

    $$h_{rad}=F_{rad}\left(T_m{}^2+T_s{}^2\right)\cdot \left(T_m+T_s\right)$$

    with

    $$F_{rad}=\frac{\sigma }{\frac{1}{{\epsilon }_1}+\frac{1}{{\epsilon }_2}-1}$$
    Where,

    $\sigma =5.669\times {10}^{-8}\left[\frac{W}{m^2{K}^4}\right]$

    Stefan Boltzman constant

    ${\epsilon }_1$

    Emissivity of secondary surface

    ${\epsilon }_2$

    Emissivity of main surface

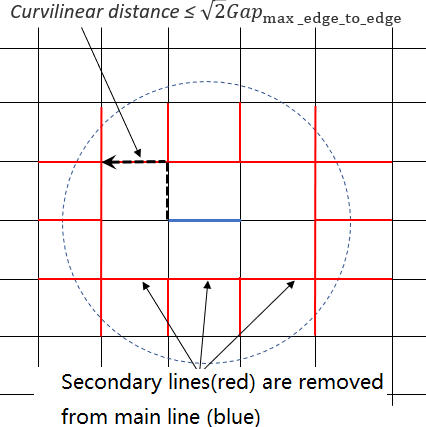
18. If the element size is less than the contact gap and there are self-impact contacts, no physical contact with neighboring secondary lines can occur. In case of self-contact, using Irem_gap=2, contact with the neighboring secondary line segments will be removed.
    For each main line, element connectivity is used to determine neighboring lines. Then secondary lines for which curvilinear distance of at least one node is less than $\sqrt{2}\cdot Gap$ (in initial configuration) are removed from the contact with this main line. The real distance between main and secondary lines is also checked to verify that all neighboring lines are removed.