The Linear Elastic Bonding contact model (LEBM) consists of elastic bonds, providing
a distinct type of behavior than the Bonding V2 model.
The theory presented in the articles Comparative Study of Different Discrete Element
Models and Evaluation of Equivalent Micromechanical Parameters by J. Rojek et
al. (2012) and Advances in the Development of the Discrete Element
Method for Excavation Processes by C.A. Labra (2012) served as the foundation
for the model's implementation in EDEM. It is recommended
that you refer to the aforementioned paper and thesis for an in-depth description of the
model.
The behavior of the LEBM is determined by the contact information for a certain pair of
elements, either particle-particle or particle-Geometry. The LEBM, like many other
EDEM contact models, considers both normal and
tangential (or shear) force components, with the normal direction always acting along
the line of centers of the two contacting elements and the tangential direction always
acting perpendicular to this.
The contact force F between a pair of contacting elements is decomposed into both normal
and tangential components, Fn and Ft, respectively,
as:
Where n is the unit vector along the line of centers of the two elements.
Calculating the force with active bonds
Consider the constitutive equations when the bonds are present and active, for a
given pair of elements (where subscripts 1 and 2 indicate the different
elements).
The following are calculated on a per-Time Step basis and adjusted incrementally.
The Young's modulus for element i is calculated by:
Where Gi is the Shear modulus and νi the Poisson’s ratio. A
normal spring stiffness term is calculated for the bond associated with each element
i as:
Where ri is the physical radius of element i. A single value for the
overall normal stiffness of the bond kn is defined as:
The corresponding tangential stiffness kt
is calculated as:
With these bond stiffnesses defined, the associated normal contact force of the bond
is defined as:
Where δn is the normal overlap of the contact.
This normal contact force is then damped as follows:
Where vnrel is the magnitude of the normal component of the
relative velocity between the two contacting elements and cn is the
damping coefficient defined as:
Where
e is the coefficient of restitution, m* is the equivalent
mass:
and mi is the mass of element i:
The magnitude of the tangential contact force is calculated as:
Where δt is the tangential overlap of the contact. The tangential contact
force component is not damped.
Calculating the Force with Inactive
bonds
Consider the constitutive equations and associated failure criteria
for when the bonds break or if they were never created.
The failure criteria
for the bonds can be defined as follows:
Where R
n and R
t are the
normal and Shear strengths (defined by the user). The bond will break under one of
the following conditions:
- The bond is under tension and the magnitude of the normal component of the
contact force exceeds the defined normal strength.
- The bond is under either tension or compression and the magnitude of the
tangential component of the contact force exceeds the defined shear
strength.
When under compression, bonds cannot break because of an excessive
normal contact force. This is what gives the model its elastic behavior.
In
the absence of any bonds - if they were never formed or previously met one of the
failure criteria and broke, the normal contact force is calculated only when the
contacting elements are compressed.
In this instance, the normal contact force
and associated damping force remain the same as defined
previously:
and the tangential contact force is now calculated by
first calculating a trial state:
and subtracting the friction force as given by the
Coulomb Friction law:
Where μ is the Static Coefficient of
Friction.
The actual tangential contact force Ft is then calculated
as:
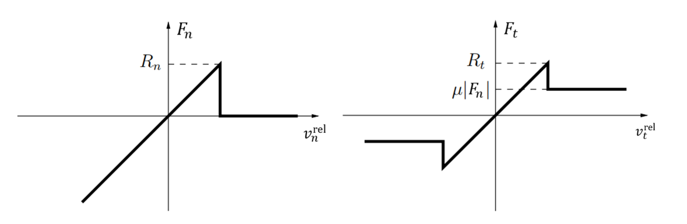
The model yields the following
force-displacement behavior:
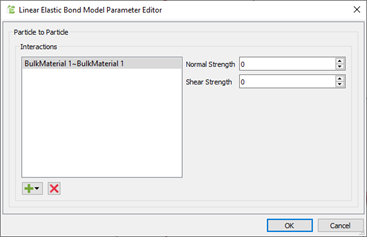
Note:
- After you have selected a list of all possible interactions for
Particle to Particle or Particle to Geometry
contacts, select the interaction for which you would like to set up
bonds.
- Specify values for Normal Strength and
Shear Strength of the formed bonds.
- Once you have specified values for the interaction, click
OK and repeat the same steps for other
interactions you would like to set up bonds for.
Post Processing
As with EDEM's Bonding V2 model, the bond properties are
post-processed by examining the characteristics of the associated contacts. For bond
visualization, it is necessary to visualize the relevant bonds and apply the
appropriate coloring.
After a simulation has run with the Linear Elastic Bonding Model enabled, you can
post process the behavior of the model using the following custom properties:
Contact custom properties
customInitialOverlap – Indicates the initial value of the
overlap of the elements in contact before the bond is formed.BondStatus – Indicates the property that determines whether
the bond exists or not. A value of 1.0 indicates a successful bond has been
formed and is currently active. A value of -1.0 indicates that the bond has
been broken. A value of 0.0 indicates a bond was never formed.customShearForce – Indicates the Shear force acting on the
contact.
Particle custom properties
customBondsInitial – Indicates the number of bonds that an
element has after the initial bond formation time.customBondsDamage – Indicates the metric for the damage to
the bonds for a given particle, calculated as:
A value of 0.0 indicates all initial bonds are still formed. A value of
1.0 indicates all initial bonds are now broken.
Simulation custom properties
customTotalBonds – Indicates the total number of bonds in
the simulation at the current Time Step. This will be at its maximum value
the Time Step after the bonds are formed and will be decremented as bonds
are broken.customBrokenBondsNormal – Indicates the total number of
bonds in the simulation that have broken due to excessive normal force.customBrokenBondsShear – Indicates the total number of
bonds in the simulation that have broken due to excessive Shear force.
Note: To activate the reporting of the following custom
properties, you must first set the environment variable
EDEM_ADDITIONAL_CUSTOM_PROPERTIES equal to 1.

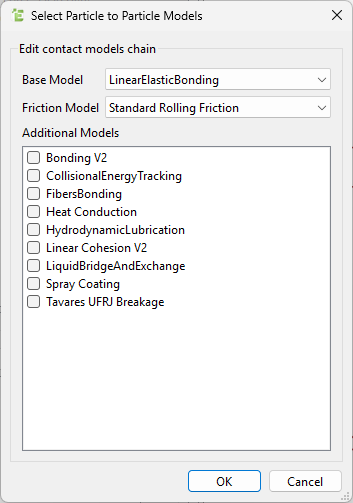
 icon in
the lower-right section of the Physics panel to configure it.
icon in
the lower-right section of the Physics panel to configure it.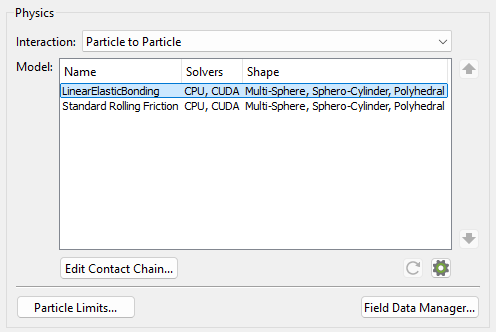
 icon to view a list of all possible
interactions for Particle-Particle or Particle-Geometry contacts.
icon to view a list of all possible
interactions for Particle-Particle or Particle-Geometry contacts.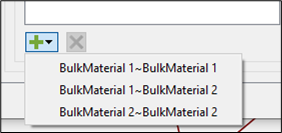
 icon
will be enabled as long as you have materials defined in your
simulation.
icon
will be enabled as long as you have materials defined in your
simulation.