構造にあるスポット溶接の疲労性能をスタディできるようにします。
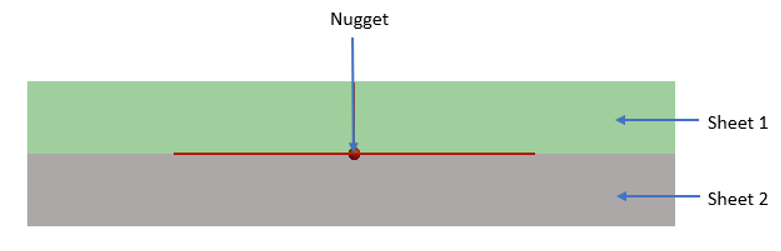
現在のところ、応力寿命(SN)に基づくスポット溶接疲労の解析のみがサポートされています。スポット溶接位置は、シート1、シート2、ナゲットの3つの属性で定義します。
Figure 1 . スポット溶接疲労
実装
スポット溶接の疲労解析では、Ruppらの論文に基づき、独立した3つの位置であるシート2か所とナゲットでの溶接を検討します。ナゲットの位置で断面に作用する力とモーメントを求め、それらを使用して、シートとナゲットの位置でそれらによって発生する応力を計算します。つづいて、これらの応力を使用し、レインフローカウントとSN法によって疲労損傷を計算します。
以降の各項では、これらの位置での応力とそれによって発生する損傷を計算する方法を取り上げます。
シート位置(1または2)
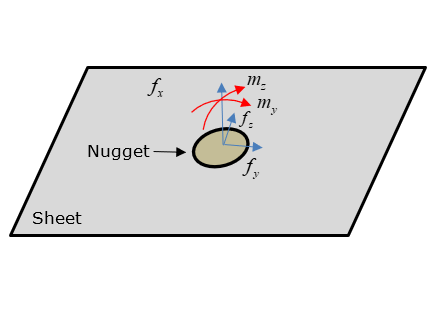
Figure 2 . シート位置で計算対象とする力とモーメント
ナゲット位置での力とモーメントを考慮することによって、シートに発生する半径方向応力を計算します。次に示す
θ
の関数として、荷重時間履歴の各時点で半径方向応力
σ
(
θ
)
ここで、
D
溶接要素の直径
T
損傷計算の対象とするシートの厚み
C
f
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGMbGaamyEaiaadQhaaeqaaaaa@39D0@
C
m
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGTbGaamyEaiaadQhaaeqaaaaa@39D7@
C
f
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGMbGaamiEaaqabaaaaa@38D0@
スケールファクター
d
e
f
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamizaiaadw
gacaWGMbGaamyEaiaadQhaaaa@3AB0@
d
e
m
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamizaiaadw
gacaWGTbGaamyEaiaadQhaaaa@3AB7@
d
e
f
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamizaiaadw
gacaWGMbGaamiEaaaa@39B0@
直径指数
t
e
f
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamiDaiaadw
gacaWGMbGaamyEaiaadQhaaaa@3AC0@
t
e
m
y
z
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamiDaiaadw
gacaWGTbGaamyEaiaadQhaaaa@3AC7@
t
e
f
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaWcbaGaamiDaiaadw
gacaWGMbGaamiEaaaa@39C0@
厚み指数
Rupp法と同等にするには:
C
f
y
z
=
1
,
d
e
f
y
z
=
0
,
t
e
f
y
z
=
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGMbGaamyEaiaadQhaaeqaaOGaaGPaVlabg2da9iaaykW7
caaIXaGaaiilaiaaykW7caaMf8UaamizaiaadwgacaWGMbGaamyEai
aadQhacaaMc8Uaeyypa0JaaGPaVlaaicdacaGGSaGaaGzbVlaadsha
caWGLbGaamOzaiaadMhacaWG6bGaaGPaVlabg2da9iaaykW7caaIWa
aaaa@57E9@
C
m
y
z
=
0.6
,
d
e
m
y
z
=
0
,
t
e
m
y
z
=
0.5
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGTbGaamyEaiaadQhaaeqaaOGaaGPaVlabg2da9iaaykW7
caaIWaGaaiOlaiaaiAdacaGGSaGaaGPaVlaaywW7caWGKbGaamyzai
aad2gacaWG5bGaamOEaiaaykW7cqGH9aqpcaaMc8UaaGimaiaacYca
caaMf8UaamiDaiaadwgacaWGTbGaamyEaiaadQhacaaMc8Uaeyypa0
JaaGPaVlaaicdacaGGUaGaaGynaaaa@5AE0@
C
f x
= 0.6 , d e f x = 0 , t e f x = 0.5
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGMbGaamiEaaqabaGccaaMc8Uaeyypa0JaaGPaVlaaicda
caGGUaGaaGOnaiaacYcacaaMc8UaaGzbVlaadsgacaWGLbGaamOzai
aadIhacaaMc8Uaeyypa0JaaGPaVlaaicdacaGGSaGaaGzbVlaadsha
caWGLbGaamOzaiaadIhacaaMc8Uaeyypa0JaaGPaVlaaicdacaGGUa
GaaGynaaaa@57CB@
相当半径方向応力を、
θ
(デフォルトでは18°)の間隔で計算します。
θ
の値は、スポット溶接の解設定でNumber of angles欄を編集することで変更できます。つづいて、レインフロー周期カウントを使用し、角度位置(
θ
ナゲット位置
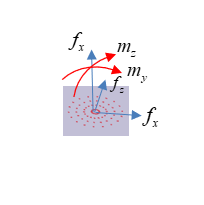
Figure 3 . ナゲット断面で計算対象とする力とモーメント
ビーム要素に作用するせん断応力と曲げ応力を使用して、次のように
θ
の関数として絶対最大主応力を荷重時間履歴の各時点で計算します。
τ
(
θ
)
=
τ
max
(
f
y
)
sin
θ
+
τ
max
(
f
z
)
cos
θ
ここで、
τ
max
(
f
y
)
=
16
f
y
3
π
D
2
τ
max
(
f
z
)
=
16
f
z
3
π
D
2
σ
max
(
m
y
)
=
32
m
y
π
D
3
σ
max
(
m
z
)
=
32
m
z
π
D
3
D
溶接要素の直径
T
損傷計算の対象とするシートの厚み
等価最大絶対主応力は、
τ
(
θ
)
σ
(
θ
)
θ
で計算されます。これらの応力を以降の疲労解析で使用します。レインフロー周期カウントを使用して、角度の
θ