動解析

SimSolidの動解析を使用して、リアルタイムで設計を評価します。

設定

解析のリンク先とするモーダル結果を指定します。現在の設計スタディにモーダル解が存在している必要があります。SimSolidでは、運動方程式の時間積分をきわめて高速で演算できるので、すべてのモードが必ず解析の対象になります。
周波数応答とランダム応答を求める場合は、周波数間隔と下限を指定します。非定常応答については、時間間隔を指定してください。
応答スペクトル解析では、モーダルの組み合わせタイプを指定します。CQC法を選択した場合、減衰比が必要です。
レイリー減衰係数またはモーダル減衰を使用して減衰を指定します。
解析の段階でピーク応答を評価するには解析時にすべてのピーク応答を評価するチェックボックスを選択します。

詳細は解析の作成を参照してください。

減衰

2種類の方法で減衰を指定できます。

レイリー減衰係数: 減衰マトリックスが質量マトリックスと剛性マトリックスに比例すると仮定します。この方法を使用するには、動的作成のダイアログで質量（F1）と剛性（F2）の値を指定する必要があります。
モーダル減衰: モードごとに限界減衰率を作成します。この値は動的解析作成のダイアログで指定できます。

動的解析に関する註

基礎励振のタイプが変位の場合、初期条件の変位と速度は必ずゼロです。
SimSolidでは、境界の互換性がほぼ満たされています。拘束された端での応答は、絶対値でゼロにはなりませんが、ピーク応答と比較して相対的に小さい値になります。
等価放射出力密度は次のように計算されます。
$ERP Density = ERPRLF * (0 .5 * ERPC * ERPRHO) * v^{2}$
ここで、

$v$

選択したポイントの法線速度

ERPC（空気中の音速）

343 m/s

ERPRHO（空気の密度）

1.225Kg/m3

ERPRLF（放射損失率）

1

等価放射出力は、選択したフェイス全体にわたるERP密度の積分として次のように計算されます。
$ERP = ERPRLF * (0 .5 * ERPC * ERPRHO) \int_{S} v^{2} d s$
絶対変位の位相は、周波数動解析でPick Infoを使用して問い合わせることができます。
周波数動解析における相対変位と絶対変位の関係を以下に示します。
相対運動は次のように計算されます：
$\ddot{x} + 2 ζ ω_{n} \dot{x} + ω_{n}^{2} = - \ddot{b}$
ここで、基礎励振 $b$ は次のとおりです：
$- \ddot{b} = Y_{0} (ω) e^{i (ω t + ϕ)}$
この微分方程式の解、相対変位は次のように計算できます：
$x_{r} (t) = Y_{0} (ω) e^{i ϕ} (\frac{ω_{n}^{2} - ω^{2}}{{(ω_{n}^{2} - ω^{2})}^{2} + {(2 ζ ω_{n} ω)}^{2}} - i \frac{2 ζ ω_{n} ω}{{(ω_{n}^{2} - ω^{2})}^{2} + {(2 ζ ω_{n} ω)}^{2}}) e^{i ω t}$

Note: 絶対運動は、相対運動と基礎励振の合計によって計算されます。
周波数動解析とランダム動解析では、複素関数法を使用して微分方程式が解かれます。変位、速度、および加速度の結果に複素成分が含まれます。
変位の複素値が次のように与えられた場合：
$D_{x} = a_{x} + i b_{x}$
$D_{y} = a_{y} + i b_{y}$
$D_{z} = a_{z} + i b_{z}$
$D_{x}$ の大きさと位相を次の式で評価します：
$M a g (D_{x}) = |D_{x}| = \sqrt{{a_{x}}^{2} + {b_{x}}^{2}}$
$P h a (D_{x}) = θ_{x} = \tan^{- 1} \frac{b_{x}}{a_{x}}$
同様に $D_{y}$ および $D_{z}$ についても同様の式が適用されます。SimSolidで、 $|D_{x}|$ および $θ_{x}$ がエクスポートされます。
$a_{x}$ と $b_{x}$ を以下の式で評価することができます：
$a_{x} = |D_{x}| \cos θ_{x}$
$b_{x} = |D_{x}| \sin θ_{x}$
変位量は次のように計算されます：
$|\sqrt{D_{x}^{2} + D_{x}^{2} + D_{x}^{2}}| = \sqrt{|D_{x}^{2} + D_{x}^{2} + D_{x}^{2}|}$
以下の式が使用され、
${D_{x}}^{2} + {D_{y}}^{2} + {D_{z}}^{2} = {a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2} + i 2 (a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z})$
以下を求めることができます：
$|{D_{x}}^{2} + {D_{y}}^{2} + {D_{z}}^{2}| = \sqrt{{({a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2})}^{2} + {(2 (a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}))}^{2}} = \sqrt{{({a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2})}^{2} + A}$
ここで、
$A = - 4 ({a_{x}}^{2} {b_{y}}^{2} + {a_{y}}^{2} {b_{x}}^{2} + {a_{x}}^{2} {b_{z}}^{2} + {a_{z}}^{2} {b_{x}}^{2} + {a_{y}}^{2} {b_{z}}^{2} + {a_{z}}^{2} {b_{y}}^{2} - 2 a_{x} b_{x} a_{y} b_{y} - 2 a_{x} b_{x} a_{z} b_{z} - 2 a_{y} b_{y} a_{z} b_{z})$
例：
$D_{x} = 1 + 2 i, D_{y} = 3 + 4 i, D_{z} = 1.5 + 3.5 i$
変位量：44.5
非定常動解析が初期応力モーダル解析にリンクされている場合は、全変位という新しい結果タイプが提供されます。全変位は、初期応力変位と動的変位の組み合わせです。そのため、変位量は動解析によって引き起こされた変位です。
ランダム応答解析の場合、応答のパワースペクトル密度（PSD） $S_{x o} (f)$ は、音源のパワースペクトル密度 $S_{a} (f)$ と以下のような関連を持ちます：
$S_{x o} (f) = {|H_{x a} (f)|}^{2} S_{a} (f)$
ここで $H_{x a} (f)$ は周波数応答関数。
理解を深めるため、ここで、ランダム応答解析の入力として、加速度を励振タイプとする基礎励振を例にとります。
振幅を持つ基本励振は、周波数応答解析の入力を定義するために使用され、加速度励振タイプの単位は、以下の強調表示された単位、m/sec²、mm/sec²、cm/sec²、G、in/sec²のいずれかになります。
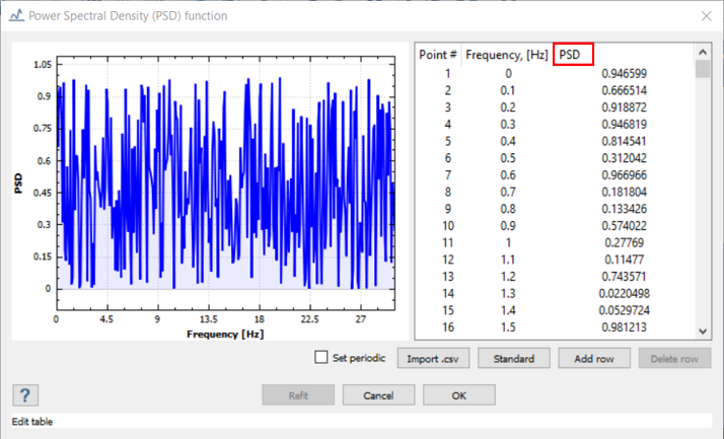
PSD関数の単位は境界条件によって異なります。この例では、基礎励振が加速度として与えられているため、PSDの単位は (mm/s²)²/Hzなります。
Figure 1.