損傷モデル選択に関する基本的な基準ランダム応答疲労解析

ランダム応答解析から得られたパワースペクトル密度（PSD）の結果は、応力範囲に対するサイクル数の確率密度関数を生成するために使用されるモーメント $m_{n}$ の計算に使用されます。

PSDモーメントは、ランダム応答解析から生成されたPSD応力をもとに算出されます。

パワースペクトル密度(PSD)モーメント

PSDモーメントは、ランダム応答解析で生成されたPSD応力をもとに、次のように計算されます：

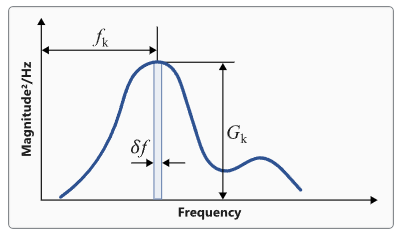
以下を元にモーメントを算出します：

$m_{n} = \sum_{k = 1}^{N} f_{k}^{n} G_{k} δ f$

ここで、

$f_{k}^{}$: 周波数値。
$G_{k}$: 周波数 $f_{k}^{}$ での PSD 応答値。

応力範囲の発生確率の計算

各Binセクション内の初期応力範囲値と最終応力範囲値の間の応力範囲の発生確率をユーザー定義で計算します。

$(Δ S_{i} - δ S / 2)$ と $(Δ S_{i} + δ S / 2)$ の間に発生する応力範囲の確率 $P (Δ S_{i})$ ：

$P (Δ S_{i}) = p δ S_{i}$

確率密度関数（応力範囲に対するサイクル回数の確率密度）

上記のように算出されたPSDモーメントは、応力範囲の確率密度関数 $f (m_{n})$ の生成に使用されます。この関数は、指定された損傷モデルに基づいています。損傷モデルを定義するために、DIRLIK、LALANNE、NARROW、Steinberg 3 band（THREE）のオプションが用意されています。

DIRLIK: DIRLIKは、確率密度関数を決定するための閉形式の解を次のように仮定します：
$p (S) = \frac{\frac{D_{1}}{Q} e^{\frac{- Z}{Q}} + \frac{D_{2} Z}{R_{2}} e^{\frac{- Z^{2}}{2 R^{2}}} + D_{3} Z e \frac{- Z^{2}}{2}}{2 \sqrt{m_{0}}}$; ここで、

$D_{1} = \frac{2 (x_{m} - γ^{2})}{1 + γ^{2}}$

$D_{2} = \frac{1 - γ - D_{1} + D_{1}^{2}}{1 - R}$

$D_{3} = 1 - D_{1} - D_{2}$

$Z = \frac{S}{2 \sqrt{m_{0}}}$

$Q = \frac{1.25 (γ - D_{3} - D_{2} R)}{D_{1}}$

$R = \frac{γ - x_{m} - D_{1}^{2}}{1 - γ - D_{1} + D_{1}^{2}}$

$x_{m} = \frac{m_{1}}{m_{0}} \sqrt{\frac{m_{2}}{m_{4}}}$

$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$

不規則性係数。

$S$

応力範囲。
LALANNE: LALANNEランダム疲労損傷モデルは、確率密度関数を次のように表現しています：
$p (S) = \frac{1}{\sqrt{m_{0}}} \frac{\sqrt{1 - γ^{2}}}{\sqrt{2 π}} e^{\frac{- S^{2}}{8 m_{0} (1 - γ^{2})}} + \frac{S_{γ}}{4 \sqrt{m_{0}}} (1 + e r f (\frac{S γ}{2 \sqrt{2 m_{0} (1 - γ^{2})}}))$; ここで、

$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$

不規則性係数。

$S$

応力範囲。
NARROW: 狭帯域ランダム疲労損は、以下の確率関数を使用します：
$p (S) = (\frac{S}{4 m_{0}} e^{- (\frac{S^{2}}{8 m_{0}})})$; ここで、

$S$

応力範囲。; デフォルトでは、狭帯域には、ゼロクロッシング数 $n_{p e a k s} = \sqrt{m_{4} / m_{2}}$ はピーク数 $n_{z c r o s s} = \sqrt{m_{2} / m_{0}}$ の代わりに使用されます。これは、 $m_{4}$ を含む数値計算が不安定な数値挙動につながることがあるためです。理想的な狭帯域であれば、ゼロクロッシングの数とピークの数はほぼ同じになるはずです。
THREE: Steinberg 3-band ランダム疲労損傷モデルは、以下の確率関数を使用します：
$P (S) = \{\begin{matrix} 0.683 a t 2 \sqrt{m_{0}} \\ 0.271 a t 4 \sqrt{m_{0}} \\ 0.043 a t 6 \sqrt{m_{0}} \end{matrix}$; ここで、

$S$

応力範囲。; 他の損傷モデルとは異なり、THREEバンドでは、これらの値は確率（確率密度ではない）です。これは、他の損傷モデルの下域 $p (S)$ に対して、上域 $P (S)$ を使用していることからも明らかです。; THREE損傷モデルの場合、これらの確率は、 $P (S)$ を、全時間履歴におけるゼロクロッシングの総数とかけることで、サイクル数を計算するために直接使用されます。他のダメージモデル（THREEを除く）では、まず確率密度値に $D S$ （Binサイズ）をかけることで確率を求めます。

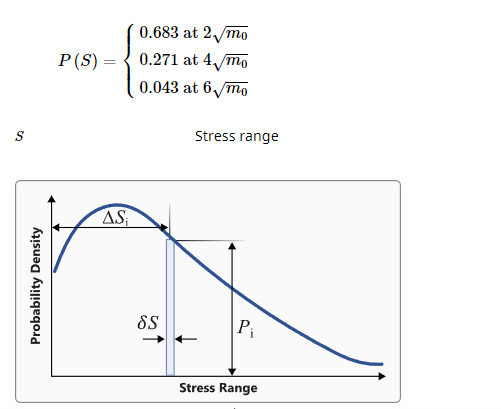
Figure 2. 確率密度関数. 応力範囲に対するサイクル回数の確率密度; 確率密度関数は、ランダム応答疲労解析の設定で定義された以下のパラメータに基づいて調整することができます。

上限応力範囲係数

応力範囲の上限の算出：

応力範囲上限値＝ 2 * RMS応力 * 応力範囲上限値係数

ランダム応答サブケースからRMS応力を出力します。対象となる応力範囲は、応力範囲の上限値で制限されます。上限を超える応力は、ランダム疲労損傷の計算では考慮されません。

上限応力範囲

上限応力範囲を直接指定します。

Bin数

確率が算出される応力範囲 $D S = δ S$ の幅を算出する（図 2参照）。デフォルトは100で、最初のBinは0.0から $δ S$ までです。応力範囲の幅は、DS=上限応力範囲/Bin数として計算されます。

応力範囲幅

応力範囲幅( $δ S$ )を直接定義します。

応力範囲の発生確率の計算

各Binセクション内の初期応力範囲値と最終応力範囲値の間の応力範囲の発生確率は、損傷モデルに基づいて計算されます。

DIRLIK, LALANNE, NARROW: $(Δ S_{i} - δ S / 2)$ と $(Δ S_{i} + δ S / 2)$ の間に発生する応力範囲の確率 $P (S_{i})$ ：
$P (S_{i}) = p_{i} (S_{i}) δ S$
THREE: 式 6をご参照ください。; THREE損傷モデルの場合、Binは3つのみです。各応力範囲（2*RMS、4*RMS、6*RMS）におけるサイクル数は、対応する確率にゼロクロッシングの総数を直接乗じて算出します（ゼロクロッシングの算出については下記をご参照ください）。

損傷モデルの選択

損傷モデル選択に関する基本的な基準：

応力のPSDモーメントから対応するモーメントを算出し、これを用いて応力範囲の確率密度関数を決定します。
DIRLIKとLALANNEモデルは、より広い応力範囲スペクトラム分布での確率を生成します。したがって、これらのモデルは、入力されるランダム信号が複数の周波数にわたる様々な応力範囲で構成されている場合に適しています。DIRLIKとLALANNEを使用した場合の確率密度関数の情報は、応力範囲分布のより広い範囲を把握できます。
NARROWモデルは、応力範囲が特定の応力範囲分布と高い確率で密接に関連すると予想されるランダム信号に使用使用することを想定しています。したがって、入力されたランダムデータの応力範囲分布が広くなく、主に特定の応力範囲に分布が集中している場合、NARROWの使用が適しています。このモデルでは、特定の応力範囲に最も高い確率で応力範囲が存在すると予想されます。
THREEモデルはNARROWモデルと似ていますが、ランダム信号の分布に、1*RMSとの関連に加え、2*RMS、3*RMSとの関連もある程度含まれると予想されます。したがって、入力されたランダムデータが主に1*RMSの応力範囲に集まっており、さらに少ないながらも2*RMS、3*RMSに関係してくる場合は、THREEの使用が適しています。

ピーク数とゼロクロッシング

NARROW、THREE: オリジナルの時間領域ランダム荷重（ここから周波数ベースのランダムPSD荷重が生成される）の1秒あたりのゼロクロッシングの数は、次のように決定されます：
$n_{z c r o s s} = \sqrt{\frac{m_{2}}{m_{0}}}$
ここで、

$m_{n}$

対応するモーメントが計算されます。
DIRLIK、LALANNE: オリジナルの時間領域ランダム荷重（ここから周波数ベースのランダムPSD荷重が生成される）の1秒あたりのピーク数は、次のように決定されます：
$n_{p e a k s} = \sqrt{\frac{m_{4}}{m_{2}}}$
ここで、

$m_{n}$

対応するモーメントが計算されます。

サイクル数

NARROW、THREE: サイクルの総数を次の式から求めます：
$N_{T} = n_{z c r o s s} T$
ここで、

T

暴露時間。
DIRLIK、LALANNE: サイクルの総数を次の式から求めます：
$N_{T} = n_{p e a k s} T$
ここで、

T

暴露時間。
特定応力範囲における総サイクル数: 応力範囲 $Δ S_{i}$ を持つ総サイクル数は、次のように計算されます：
$N_{i} = P (Δ S_{i}) N_{T}$

疲労寿命と損傷

疲労寿命（材料が破壊するまでの特定の応力範囲 $S_{i}$ の最大サイクル数）は、材料SN曲線に基づいて次のように計算されます：

$N_{f} (S_{i}) = {(\frac{S_{i}}{S_{f}})}^{\frac{1}{b}}$

適用されたランダム荷重の結果としてのトータルの疲労損傷は、次のように計算されます：

$D = \sum_{i = 1}^{N} \frac{N_{i}}{N_{f} (S_{i})}$

平均応力がゼロとならない荷重による平均応力補正を考慮するために、そのような荷重（通常は重力荷重）からなる静的サブケースを定義することができます。この静的サブケースは、ランダム疲労解析のイベント設定で参照することができます。