疲労材料データのばらつき

疲労テスト結果のばらつきを扱います。

材料のSN曲線とEN曲線（および他の疲労特性）は、回転曲げ試験によって実験的に得られます。通常はテスト結果に大きなばらつきが伴うことから、データの統計的な特性記述も入手する必要があります（耐久確実性を使用し、曲線の標準誤差に応じてlog(N)の平均値の最悪値を推測します。高水準の信頼性を実現するには高い耐久確実性が必要です）。

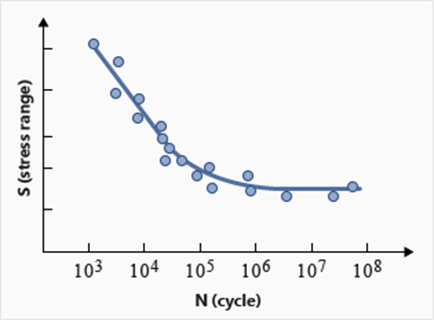
このようなパラメータを把握するために、SN曲線の例を考察します。周期的に変化する公称応力振幅S_aまたはその範囲S_Rおよび破壊に至るまでの周期数Nを両軸として、両対数スケールでSNテストデータをプロットすると、SとNとの関係を複数の線分で表すことができます。通常は、1本または2本の線分で理想化します。

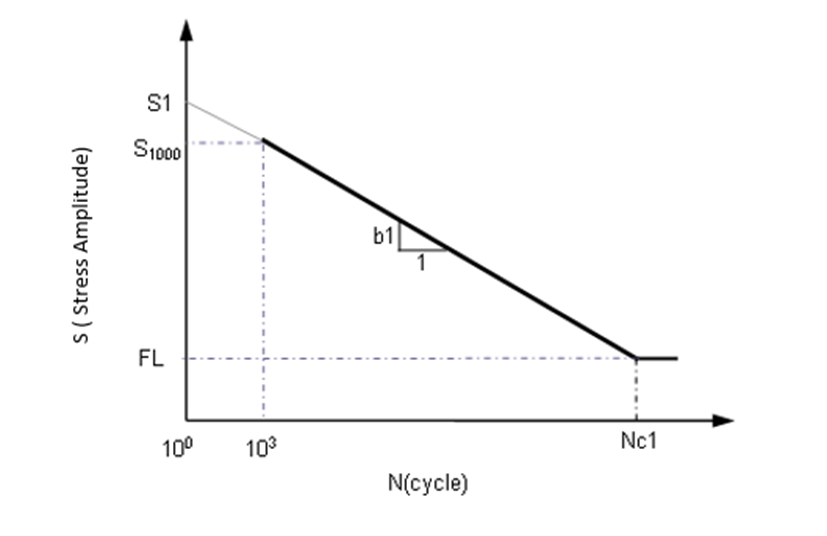
同じ材料の同じ試験片で得られると考えられるSN曲線が、SNのばらつきによって変動する状況を考えます。両振り逆回転曲げテストの結果では、多くの場合、自然変動によって応力振幅（S）と寿命（N）の両方のデータ点が変動しています。対数スケールで見ると、Log(S)とLog(N)にいくつかの変動があります。具体的には、同じ応力振幅を適用した状態で寿命に現れる変動に注目すると、そのデータ点は次のようになります。


S	Log (S)	Log (N)
2000.0	3.3	3.9
2000.0	3.3	3.7
2000.0	3.3	3.75
2000.0	3.3	3.79
2000.0	3.3	3.87
2000.0	3.3	3.9

多くのプロセス同様、Log(N)の分布は正規分布であると見なされます。log(S)の特定の値に対してlog(N)が示すと考えられる値の全集合が存在します。この全集合の平均値が真の母平均となりますが、それを知ることはできません。したがって、入力したサンプルデータの平均値（SN曲線）とサンプルデータの標準誤差（SE）に基づいて、log(N)の真の母平均の最悪値を統計的に推測します。SNの材料データ入力は、そのデータの生成に使用した特定サンプルのばらつきが示す正規分布の平均に基づきます。

Figure 3. ユーザーが定義した特定サンプルデータにあるSNのばらつきによってLog(N)が示す正規分布の確率関数

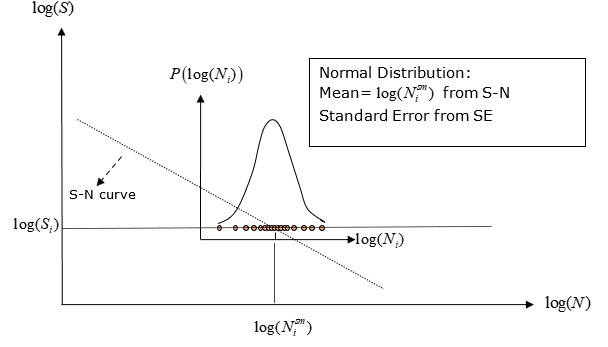
応力振幅データと寿命データの両方に実験上のばらつきが存在します。入力としてlog(N)の散乱の標準誤差が必要です（SN曲線のSE欄）。サンプルデータの平均値はSN曲線によって $\log (N_{i}^{s m})$ として得られますが、標準誤差はSE欄に入力します。

SN曲線をそのまま使用し、摂動を適用しない場合は、サンプルデータの平均値を直接使用します。これにより、50％の耐久確実性が得られます。これは、指定したサンプルデータの平均値に摂動が発生しないようにするということです。すべての用途で50％の耐久確実性が十分であるとはいえないので、SimSolidでは、ユーザーが指定した目的の耐久確実性の範囲でSN材料データに対して内部的に摂動を適用できます。そのためには、次のデータが必要です：

log(N)の正規分布の標準誤差（SE）
実施する解析に必要な耐久確実性

正規分布（ガウス分布）は確率密度関数であり、曲線の下を占める総面積が必ず1.0に等しくなります。

ユーザーが指定するSN曲線データは正規分布と見なされるので、多くの場合、その特性は次の確率密度関数で記述できます。

$P (x_{s}) = \frac{1}{\sqrt{2 π σ_{s}^{2}}} e^{- \frac{{(x_{s} - μ_{s})}^{2}}{2 σ_{s}^{2}}}$

各値の意味は次のとおりです：

$x_{s}$ ：定義したサンプルにあるデータ値（ $\log (N_{i})$ ）

$μ_{s}$ ：サンプルデータの平均値（ $\log (N_{i}^{s m})$ ）

$σ_{s}$ ：サンプルデータの標準偏差（標準誤差（SE）のみを入力しているので不明）

上記の分布はユーザーが指定した分布であり、全集団空間ではありません。真の母平均は不明なので、サンプルデータの平均値とサンプルデータのSEから真の母平均の範囲を推定したうえで、ユーザーが定義した耐久確実性を使用してサンプルデータの平均値に摂動を適用します。

標準誤差は、全集合から導いたサンプルのすべてのサンプルデータ平均値によって作成した正規分布の標準偏差です。1件のサンプル分布データについて、多くの場合、標準誤差は $S E = (\frac{σ_{s}}{\sqrt{n_{s}}})$ と推定されます。 $σ_{s}$ はサンプルの標準偏差、 $n_{s}$ はサンプルにあるデータ値の数です。実際には、すべてのサンプルデータ平均値のこの分布の平均値が、真の母平均と同じになります。すべてのサンプルデータ平均値のこの分布に、指定した耐久確実性が適用されます。

一般的には、正規分布関数を標準正規分布曲線（平均値が0.0、標準誤差が1.0の正規分布）に変換します。これにより、標準正規分布表（Z値分布表）から耐久確実性の値を直接使用できます。

Note: 耐久確実性の値は、目的のサンプル間で確率密度関数曲線の下を占める面積に等しくなります。この正規分布曲線の面積を（標準正規分布曲線に変換せずに）計算で直接求めることもできますが、Z値分布表による方法に比べると計算に手間を要します。したがって、一般的には、まず手元の正規分布を標準正規分布に変換したうえで、Z値分布表を使用して、指定する耐久確実性をパラメータ化します。

すべてのサンプルデータ平均値の正規分布についていえば、その分布の平均値が真の母平均 $μ$ と同じになります。推定しようとしている値は、この真の母平均の範囲です。

統計的には、次の式で真の母平均の範囲を推定できます。

$\log (N_{i}^{s m}) - z * S E \leq μ \leq \log (N_{i}^{s m}) + z * S E$

これは次のようになります。

$\log (N_{i}^{s m}) - z * S E \leq \log (N_{i}^{m}) \leq \log (N_{i}^{s m}) + z * S E$

この式の左辺は控え目な値になるので、次の式を使用してSN曲線に摂動を適用します。

$\log (N_{i}^{m}) = \log (N_{i}^{s m}) - z * S E$

各値の意味は次のとおりです：

$\log (N_{i}^{m})$ ：適用する摂動の値

$\log (N_{i}^{s m})$ ：定義したサンプルデータ平均値（SN曲線）

$S E$ ：標準誤差（SE）

$z$ の値は、指定する耐久確実性の値に基づいてZ値分布表から取得します。Z値分布表上で耐久確実性に対応する一般的なZ値を、次の表にいくつか示します。


Z値（計算値）	耐久確実性（入力値）
0.0	50.0
-0.5	69.0
-1.0	84.0
-1.5	93.0
-2.0	97.7
-3.0	99.9

目的の耐久確実性と標準誤差の入力に応じてSN曲線が変化することがわかります。この手法を使用することで、統計的方法によって疲労材料データのばらつきを扱い、目的とする耐久確実性の値に見合うデータを予測できます。