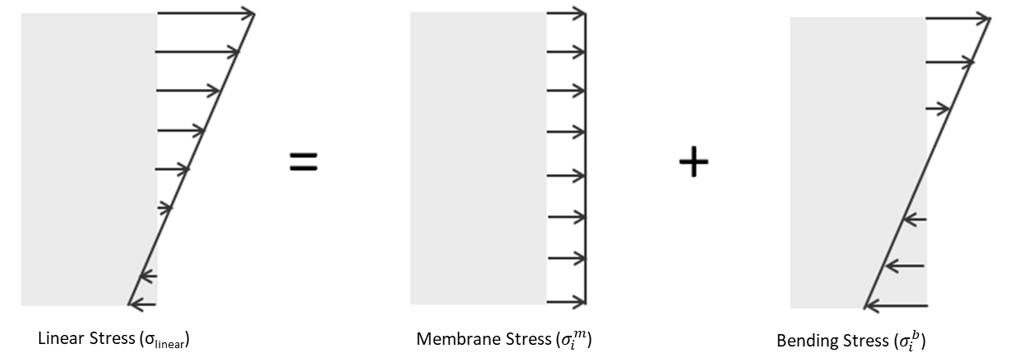
SimSolid に実装されているシーム溶接の疲労は、Volvoメソッドと組み合わされた応力の線形化に基づき、疲労損傷と寿命を予測します。線形化応力は、板厚方向の弾性応力場を、同等の膜応力と曲げ応力に分解します。
この手法では、総応力に対する曲げの寄与が求められ、その値からその溶接が本質的に剛性が高いのか弾性が高いのかが決まります。この手法では一般に2つのS-N曲線が必要です。1つは曲げ応力が優勢な曲げS-N曲線で、もう1つは膜応力が優勢な膜S-N曲線です。曲げの度合に応じて、曲げS-N曲線と膜S-N曲線の間で補間が行われます。
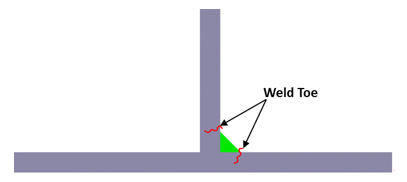
溶接止端部の破壊(疲労亀裂)の予測位置または可能性のある位置がマークされます。これらの場所について、疲労損傷が評価されます。
Figure 1 . 破壊の可能性のある位置を示すフィレット溶接の断面
溶接応力の計算
SimSolid でのシーム溶接の疲労損傷の計算では、応力線形化手法(
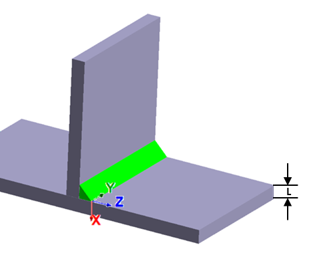
SimSolid の線形化応力ドキュメントにリンク)とその応力に関連付けられた曲げ比を利用して、対象の位置での構造応力を使用します。線形化応力は、ローカル座標系で応力線形化セグメントに沿って求められます。ローカル座標系は、
Figure 2 に示すように、セグメントの開始ポイントと終了ポイントを基準にしています。ローカル座標系のX軸は、開始ポイントから終了ポイントまでのセグメントに沿っています。他の2つの軸は以下のように計算されます:
Figure 2 . 上記の抽出された応力値から、数値積分を使用して、平均膜応力テンソルと開始ポイントと終了ポイントでの終点曲げ応力テンソルが計算されます。
ここで、
σ
i
m
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadMgaaeaacaWGTbaaaaaa@39C3@
i
t
h
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAamaaCa
aaleqabaGaamiDaiaadIgaaaaaaa@38F4@
成分です。
σ
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaadMgaaeqaaaaa@38D0@
i
t
h
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAamaaCa
aaleqabaGaamiDaiaadIgaaaaaaa@38F4@
σ
i
S
b
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadMgacaWGtbaabaGaamOyaaaaaaa@3A90@
i
t
h
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAamaaCa
aaleqabaGaamiDaiaadIgaaaaaaa@38F4@
σ
i
E
b
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadMgacaWGfbaabaGaamOyaaaaaaa@3A82@
i
t
h
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAamaaCa
aaleqabaGaamiDaiaadIgaaaaaaa@38F4@
成分です。
L
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamitaaaa@36C4@
i
t
h
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyAamaaCa
aaleqabaGaamiDaiaadIgaaaaaaa@38F4@
x
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaaaa@36F0@
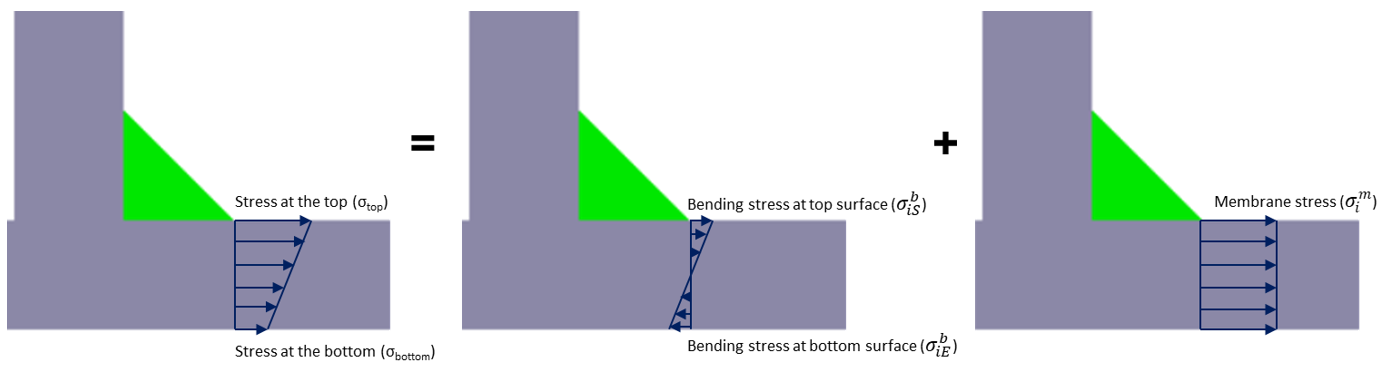
シーム溶接の損傷パラメータに使用される応力の値は、膜応力と曲げ応力の合計です。
Figure 3 . よって、上面と下面での応力は、次の式で求められます:
Note: したがって、シーム溶接解析エンジンで使用される計算方法は、ソリッドモデルまたは薄肉シェルモデルで計算された応力に同様に適用できます。これにより、上面および下面の応力が、薄肉シェルモデルで生成されるものと同じ形式で生成されます。
Figure 4 . 曲げ比(r)
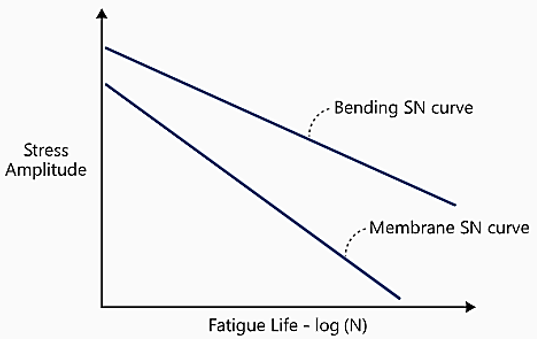
実験により、M. Fermér、M Andréasson、およびB Frodinにより提示された手法に基づいてシーム溶接の疲労解析を実行するには、2種類のSN曲線が必要であることが示されています。ラボでの試験に基づいて、2つのSN曲線がプロットされています(
Figure 5 )。上側の曲線は、最大応力が曲げモーメント優勢な試験で得られたものであり、下側の曲線は、最大応力が膜力優勢な試験で得られたものです。
Figure 5 . 上の曲線と下の曲線は、それぞれ、曲げS-N曲線、膜S-N曲線と呼ばれます。要素内で膜応力が優勢な場合は膜S-N曲線を使用し、曲げ応力が優勢な場合は曲げS-N曲線を使用することをお勧めします。曲げの優位性の度合に応じて、2つの曲線間で補間を行うこともできます。
ここで、
σ
i
b
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadMgaaeaacaWGIbaaaaaa@39B8@
6
T
2
∫
−
T
/
2
T
/
2
σ
i
x
d
x
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
aI2aaabaGaamivamaaCaaaleqabaGaaGOmaaaaaaGcdaWdbaqaamaa
DaaaleaacqGHsislcaWGubGaai4laiaaikdaaeaacaWGubGaai4lai
aaikdaaaaabeqab0Gaey4kIipakiabeo8aZnaaBaaaleaacaWGPbaa
beaakiaadIhacaWGKbGaamiEaaaa@45FD@
σ
i
m
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadMgaaeaacaWGTbaaaaaa@39C3@
1
T
∫
−
T
/
2
T
/
2
σ
i
d
x
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
aIXaaabaGaamivaaaadaWdbaqaamaaDaaaleaacqGHsislcaWGubGa
ai4laiaaikdaaeaacaWGubGaai4laiaaikdaaaaabeqab0Gaey4kIi
pakiabeo8aZnaaBaaaleaacaWGPbaabeaakiaadsgacaWG4baaaa@4408@
平均曲げ比
(
r
b
A
V
G
)
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadk
hadaqhaaWcbaGaamOyaaqaaiaadgeacaWGwbGaam4raaaakiaacMca aaa@3BCE@
は次のように定義されます:
ここで、
σ
T
O
P
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aa0
baaSqaaiaadsfacaWGpbGaamiuaaqaaiaaikdaaaaaaa@3B21@
r
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaaaa@36EA@
これは、荷重時間履歴のすべてのポイントでの曲げ比の加重平均です。
補間係数(IF)は次のように定義されます:
r
b
T
H
R
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaDa
aaleaacaWGIbaabaGaamivaiaadIeacaWGsbaaaaaa@3A7B@
r
b
A V G
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaDa
aaleaacaWGIbaabaGaamyqaiaadAfacaWGhbaaaaaa@3A6B@
r
b
T H R
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaDa
aaleaacaWGIbaabaGaamivaiaadIeacaWGsbaaaaaa@3A7B@
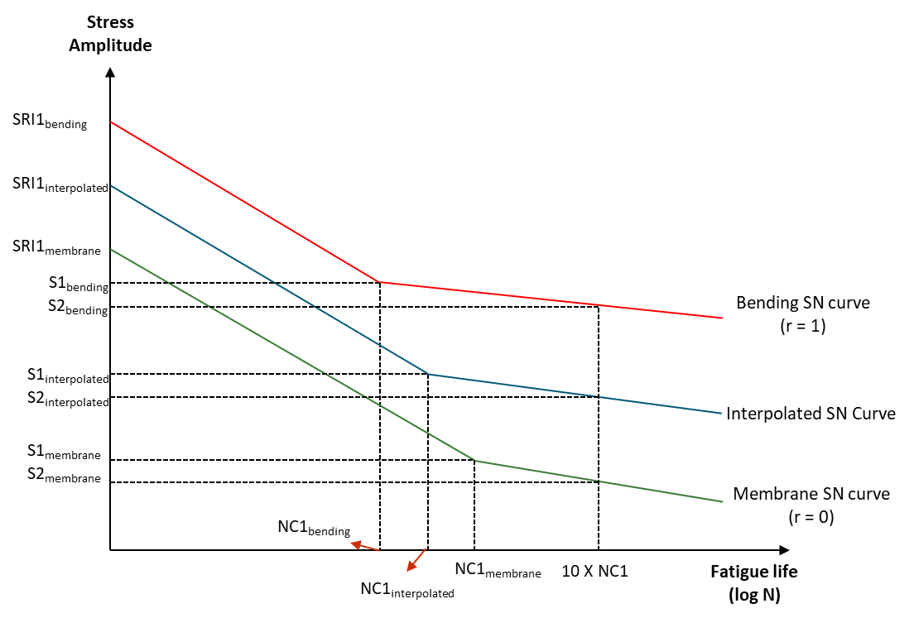
膜S-N曲線と曲げS-N曲線の間での補間
Figure 6 . Figure 6 に示す線形の補間手法では、補間係数(IF)の値が使用されます。補間曲線では、疲労強度係数(SRI1)は次のように計算されます:
interpolated = SRI1membrane + (SRI1bending – SRI1membrane ) ∙ IF
これにより、1サイクルでの応力レベルが定義されます。
interpolated = 10(log 10 Nc1 membrane + (log 10 Nc1 bending – log 10 (Nc1 membrane ) ∙IF))
interpolated = S1membrane + (S1bending – S1membrane ) ∙ IF
これは、Nc1interpolated サイクルでの応力レベルを定義します。この2点で、この曲線のNc1interpolated サイクルまでの最初のセクションが決まります。残りのセクションは、次のように3つ目のポイントを求めることによって定義されます。寿命値は、これらの剛体の曲線と弾性体の曲線のNc1値の10倍となります。これらから、S2bending とS2membrane を計算できます。これらを補間して、曲線の高サイクル部分を定義するS2interpolated が求められます。
interpolated = S2membrane + (S2bending – S2membrane ).IF
厚さ
オプションで、このパートの厚さt に基づいて、厚さ(サイズ効果補正)を適用することもできます。これは次のように機能します:
t ≤
T
r e f
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabgs
MiJkaadsfadaWgaaWcbaGaamOCaiaadwgacaWGMbaabeaaaaa@3C72@
疲労強度は
T
r
e
f
t
n
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaada
WcaaqaaiaadsfadaWgaaWcbaGaamOCaiaadwgacaWGMbaabeaaaOqa
aiaadshaaaaacaGLOaGaayzkaaWaaWbaaSqabeaacaWGUbaaaaaa@3D80@
n は、耐用期間すべてにわたって
t
>
T
r
e
f
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg6
da+iaadsfadaWgaaWcbaGaamOCaiaadwgacaWGMbaabeaaaaa@3BC5@
平均応力補正
シーム溶接の疲労ではFKM平均応力補正がサポートされています。応力感度は、fatigue solution settingsダイアログのmean stress correction欄で定義できます。シーム溶接の疲労の平均応力補正は、シーム溶接 のfatigue solution settingsダイアログで有効にできます。
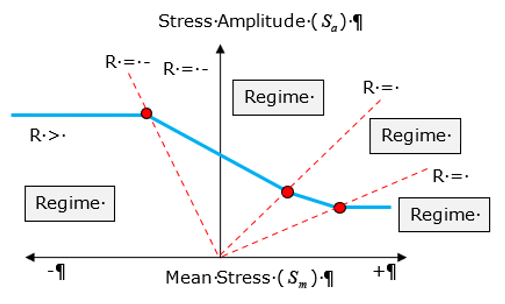
FKMのガイドラインに従い、応力比(R=Smin /Smax )の値を基準としてHaigh線図を4つの期間に分割します。次に補正値を使用して、損傷と寿命の計算段階で使用するSN曲線を選択します。
次に示すFKMの式は、補正済み応力振幅(
S
e
A
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaaaaa@38A8@
)の計算方法を示しています。損傷の計算で実際に使用する応力値は、補正済み応力振幅(
2
⋅
S
e
A
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiabgw
SixlaadofadaqhaaWcbaGaamyzaaqaaiaadgeaaaaaaa@3BAE@
)です。入力したSN曲線にこれらの式を適用します。
期間 1 (R>1.0 ):
S
e
A
=
S
a
(
1
−
M
)
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaakiabg2da9iaadofadaWgaaWcbaGa
amyyaaqabaGccaGGOaGaaGymaiabgkHiTiaad2eacaGGPaaaaa@3F7F@
期間 2 (
−
∞
≤
R
≤
0.0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0Iaey
OhIuQaeyizImQaamOuaiabgsMiJkaaicdacaGGUaGaaGimaaaa@3EB8@
S
e
A
=
S
a
+
M
*
S
m
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaakiabg2da9iaadofadaWgaaWcbaGa
amyyaaqabaGccqGHRaWkcaWGnbGaaiOkaiaadofadaWgaaWcbaGaam
yBaaqabaaaaa@4004@
期間 3 (0.0<R<0.5 ):
S
e
A
=
(
1
+
M
)
S
a
+
(
M
/
3
)
*
S
m
1
+
M
/
3
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaakiabg2da9iaacIcacaaIXaGaey4k
aSIaamytaiaacMcadaWcaaqaaiaadofadaWgaaWcbaGaamyyaaqaba
GccqGHRaWkcaGGOaGaamytaiaac+cacaaIZaGaaiykaiaacQcacaWG
tbWaaSbaaSqaaiaad2gaaeqaaaGcbaGaaGymaiabgUcaRiaad2eaca
GGVaGaaG4maaaaaaa@4A8E@
期間 4 (
R
≥
0.5
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiabgw
MiZkaaicdacaGGUaGaaGynaaaa@3ABB@
S
e
A
=
3
S
a
(
1
+
M
)
2
3
+
M
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaakiabg2da9maalaaabaGaaG4maiaa
dofadaWgaaWcbaGaamyyaaqabaGccaGGOaGaaGymaiabgUcaRiaad2
eacaGGPaWaaWbaaSqabeaacaaIYaaaaaGcbaGaaG4maiabgUcaRiaa
d2eaaaaaaa@43A5@
ここで、
S
e
A
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDa
aaleaacaWGLbaabaGaamyqaaaaaaa@38A8@
S
m
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa
aaleaacaWGTbaabeaaaaa@37E9@
M は平均応力感度です。 Figure 7 .