/MAT/LAW126 (JOHNSON_HOLMQUIST_CONCRETE)

Block Format Keyword This material law describes the behavior of brittle materials, more specifically dedicated to concrete.

Format


(1)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW126/`mat_ID`/`unit_ID` or /MAT/JOHNSON_HOLMQUIST_CONCRETE/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`G`
`a`	`b`	`n`		$f_{c}$	`T`
`c`	${\dot{ε}}_{0}$	`FCUT`		$σ_{M A X}^{*}$	$ε_{f}^{\min}$
`P`_C	$μ_{C}$	`P`_L		$μ_{L}$
`K`₁	`K`₂	`K`₃
`D`₁	`D`₂		`IDEL`	$ε_{p}^{m a x}$

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`G`	Shear modulus. (Real)	$[Pa]$
`A`	Normalized cohesive strength. (Real)
`B`	Normalized pressure hardening modulus. (Real)
`N`	Pressure hardening exponent. (Real)
$f_{c}$	Quasi-static uniaxial compressive strength. (Real)	$[Pa]$
`T`	Maximum hydrostatic tensile pressure. (Real)	$[Pa]$
`C`	Strain rate coefficient. = 0 (Default) No strain rate effect (Real)
${\dot{ε}}_{0}$	Reference strain rate. Default = 1.0 (Real)	$[\frac{1}{s}]$
`FCUT`	Cutoff frequency for strain rate filtering. = 0 No strain rate filtering (Real)	$[Hz]$
$σ_{M A X}^{*}$	Maximum normalized strength. Default = 10²⁰ (Real)
$ε_{f}^{\min}$	Minimum fracture strain. Default = 10^-20 (Real)
`P`_C	Crushing pressure. (Real)	$[Pa]$
$μ_{C}$	Crushing volumetric strain. (Real)
`P`_L	Locking pressure. (Real)	$[Pa]$
$μ_{L}$	Locking plastic volumetric strain. (Real)
`K`₁	Linear bulk stiffness. (Real)	$[Pa]$
`K`₂	Quadratic bulk stiffness. (Real)	$[Pa]$
`K`₃	Cubic bulk stiffness. (Real)	$[Pa]$
`D`₁	Damage parameter. (Real)
`D`₂	Damage exponent. (Real)
`IDEL`	Element deletion flag: = 0 (Default) No element deletion = 1 Tensile failure when $P^{} + T^{} < 0$ = 2 Failure when critical plastic strain is reached $ε_{p} > ε_{p}^{\max}$ = 3 Failure when $σ_{Y} \leq 0$ (recommended) = 4 Failure when $D = 1$ (Integer)
$ε_{p}^{m a x}$	Critical plastic strain for element deletion. Default = 10²⁰ (Real)

▸Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
Unit for material
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW126/1/1
Concrete
#        Init. dens.
            2.440E-9
#                  G
               14860
#                  A                   B                   N                  FC                   T
                0.79                1.60                0.61                  48                   4
#                  C                EPS0                FCUT               SFMAX               EFMIN
               0.007                 1.0               10000                   7                0.01
#                 PC                 MUC                  PL                 MUL
                  16               0.001                 800                 0.1
#                 K1                  K2                  K3
               85000             -171000              208000
#                 D1                  D2                IDEL             EPS_MAX
                0.04                 1.0                   3                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

This material law is based on the theory of Johnson-Holmquist-Cook model theory (also called Johnson-Holmquist-Concrete). It was proposed and designed for a concrete application. In this model, the spherical and deviatoric behavior are separated. It considers the effect of damage and strain rate sensitivity.
The spherical behavior is described with a constitutive equation based on hydrostatic pressure (considered positive in compression). This behavior is divided into 3 regions (Figure 1) in the evolution hydrostatic pressure versus volumetric strain denoted $μ$ .
$\begin{array}{l} P = \{\begin{matrix} K_{0} μ & if & P \leq P_{C} & [I] \\ (K_{0} + (K_{1} - K_{0}) \frac{μ_{p}}{μ_{L}}) (μ - μ_{p}) & if & P > P_{C} and μ_{p} \leq μ_{L} & [II] \\ K_{1} \hat{μ} + K_{2} {\hat{μ}}^{2} + K_{3} {\hat{μ}}^{3} & for the other cases & [III] \end{matrix} \\ with \\ K_{0} = \frac{P_{C}}{μ_{C}} \\ \hat{μ} = \frac{μ - μ_{L}}{1 + μ_{L}} \\ μ = \frac{ρ}{ρ_{0}} - 1 \end{array}$
In the first region, the pressure response is supposed linear and elastic. In the second region, the microcavities of the material are supposed to be crushed, generating a plastic volumetric strain denoted $μ_{p}$ , modifying linearly the bulk modulus from $K_{0}$ and $K_{1}$ . When $μ_{p} = μ_{L}$ all the cavities have been crushed and the material becomes fully dense. Then, the pressure evolution follows a polynomial equation of state.

Figure 1. Hydrostatic pressure variation with respect to volumetric strain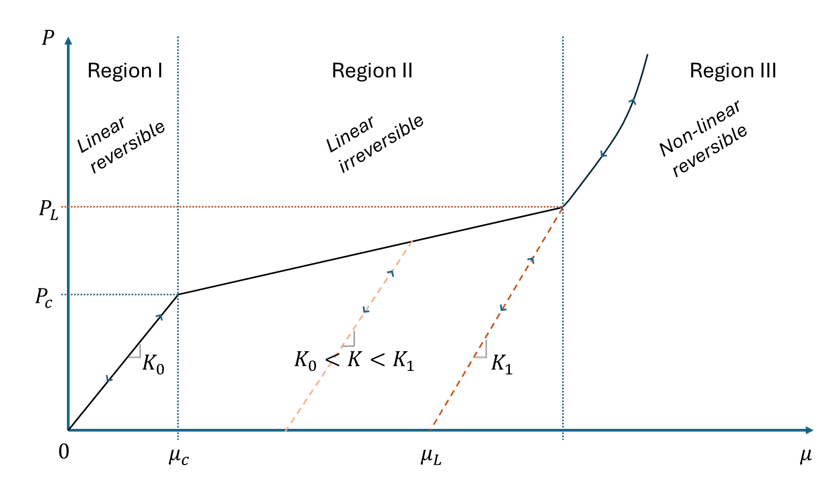
The deviatoric behavior is defined with an elasto-plastic behavior, where the normalized yield stress is both a yielding and a damaging limit. Its expression is:
- If $P^{*} > 0$ (compressive loadings):
  $σ_{Y}^{*} = \min (σ_{M A X}^{*}, (A (1 - D) + B {(P^{*})}^{N}) (1 + C {〈\ln \frac{\dot{ε}}{{\dot{ε}}_{0}}〉}_{+}))$
  Where, $P^{*} = \frac{P}{f_{c}}$ bounded by $P^{*} = - (1 - D) T^{*}$ .
- If $P^{*} \leq 0$ (tensile loadings):
  $σ_{Y}^{*} = A (1 + \frac{P}{T}) (1 - D) (1 + C {〈\ln \frac{\dot{ε}}{{\dot{ε}}_{0}}〉}_{+})$
  To get the yield stress, the normalized value is multiplied by $f_{c}$ . These two yield stresses shapes (for compressive and tension loadings) are plotted for a damage value of 0 (initial material) and 1 (fully fractured material) in Figure 2:
  
  Figure 2. Yield stress evolution with respect to hydrostatic pressure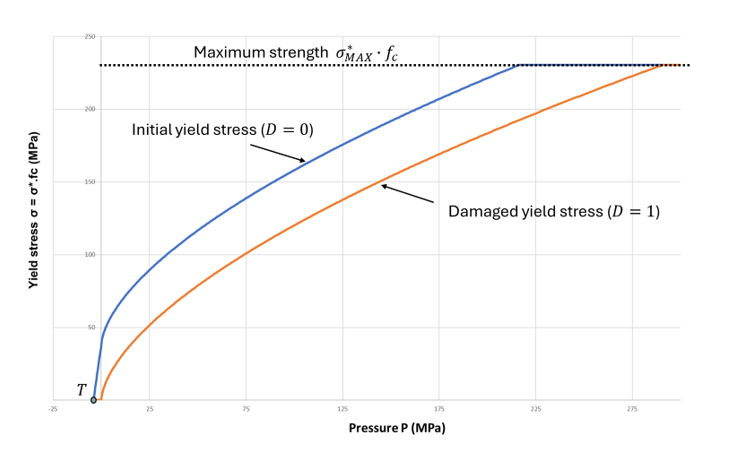
  To trigger the deviatoric elasto-plastic behavior, the normalized yield stress is compared to the current normalized equivalent von Mises stress:
  $σ_{V M}^{*} = \frac{σ_{V M}}{f_{c}}$
  This allows to compute the evolution of the deviatoric plastic strain denoted $ε_{p}$ .
The damage variable evolution is dependent to both volumetric and deviatoric plastic strain. Its expression is given by:
$D = \sum \frac{Δ μ_{p} + Δ ε_{p}}{ε_{f}^{p}}$
Where, the effective strain at failure is defined by:
$\begin{array}{l} ε_{f}^{p} = \max (D_{1} {(P^{*} + T^{*})}^{D_{2}}, ε_{f}^{\min}) \\ with P^{*} = \frac{P}{f_{c}} and T^{*} = \frac{T}{f_{c}} \end{array}$
Time history and animation output is available using these USRi variables.
- USR1: Plastic volumetric strain $μ_{p}$
- USR2: Bulking pressure $P$
- USR3: Volumetric strain $μ$
- USR4: Yield stress $σ_{Y}$
Strain rate filtering can be used and activated when a cutoff frequency FCUT for filtering is defined.
The damage variable can be plotted in ANIM and H3D file using the output option DAMG.
To avoid damage mesh dependency, due to mesh size or orientation, the non-local regularization method can be used (/NONLOCAL/MAT). In this case, the sum of the deviatoric plastic strain $ε_{p}$ and volumetric plastic strain $μ_{p}$ is regularized and used for damage evolution:
$D = \sum \frac{{(Δ μ_{p} + Δ ε_{p})}_{n l}}{ε_{f}^{p}}$
The regularized sum can be plotted using /ANIM/ELEM/NL_EPSP or /H3D/ELEM/NL_EPSP.

A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressure, G.R. Johnson, T.J. Holmquist, W.H. Cook,1993