OS-E: 0185 Rubber Ring: Crush and Slide Using Self-Contact

Model Files

Model Description

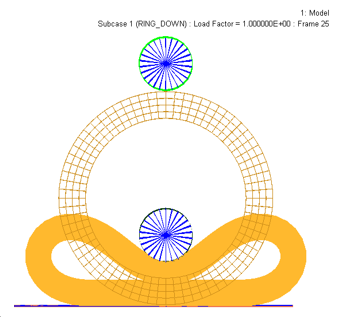
A deformed rubber ring resting on a flat, rigid surface. Another circular rigid roller rests at the top of the ring, and is in contact with the ring at just a point. Contact is defined between the rigid surfaces and the outside surface of the ring and self-contact is defined in the inside surface of the ring. The loading is applied in two steps – in the first step, the circular roller is pushed down enough to produce self-contact of the inside surface of the ring. In the second step, the roller is simultaneously translated and rotated such that the crushed ring rolls along the flat rigid surface producing a constantly changing region of contact. Here the nonlinear implicit analysis is run.

The hyperelastic material constants are obtained by conducting curve fitting with the provided TAB1 (simple tension/compression), TAB2 (biaxial tension), and TAB4 (shear) data for rubber material in the MATHE entry, during the OptiStruct run.

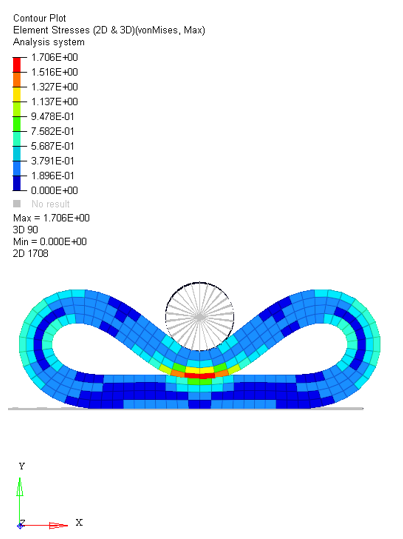
Results

Figure 2 shows the deformed shape of the rubber ring after the circular roller is pushed down enough.

Figure 2. Deformed Shape of the Rubber Ring after First Step

Figure 3 shows the slide of the crushed rubber ring along the flat rigid surface after the roller has been simultaneously translated and rotated.

Figure 3. Deformed Shape of the Rubber Ring after Second Step

Figure 4 shows the stresses in the rubber ring after it has been crushed and sliding along the flat rigid surface.

Figure 4. Stress in the Rubber Ring