Responses
The following responses can be found in this section:
Internal Responses
OptiStruct allows the use of numerous structural responses, calculated in a finite element analysis, or combinations of these responses to be used as objective and constraint functions in a structural optimization.
Responses are defined using DRESP1 Bulk Data Entries. Combinations of responses are defined using either DRESP2 entries, which reference an equation defined by a DEQATN Bulk Data Entry, or DRESP3 entries, which make use of user-defined external routines identified by the LOADLIB I/O Options Entry. Responses are either global or subcase (loadstep, load case) related. The character of a response determines whether or not a constraint or objective referencing that particular response needs to be referenced within a subcase.
Subcase Independent
Mass and Volume
Both are global responses that can be defined for the whole structure, for individual properties (components) and materials, or for groups of properties (components) and materials.
It is not recommended to use mass and volume as constraints or objectives in a topography optimization. Neither is very sensitive towards design modifications made in a topography optimization.
In order to constrain the mass or volume for a region containing a number of properties (components), the SUM function can be used to sum the mass or volume of the selected properties (components), otherwise, the constraint is assumed to apply to each individual property (component) within the region. Alternatively, a DRESP2 equation needs to be defined to sum the mass or volume of these properties (components). This can be avoided by having all properties (components) use the same material and applying the mass or volume constraint to that material.
RTYPE=VOLUME and ATTA=ENCLOSED can be used to create an enclosed volume response for Shape, Free-Shape, and Topography optimization. The ENCLOSED option indicates that this response is an enclosed volume defined by a closed 2D mesh (free-edges are not supported). For this enclosed volume response type, ATTI field(s) should be set to PID. Multiple ATTi are allowed, as long as the mesh defined by the PID's is fully enclosed. The property type should be PSHELL, PCOMP, or PSHEAR only. The normals of the 2D mesh should be oriented consistently and the mesh should be sufficiently fine to capture the volume data. The volume is calculated based on the mesh and it is not recommended to use a coarse mesh.
Fraction of Mass and Fraction of Design Volume
Both are global responses with values between 0.0 and 1.0. They describe a fraction of the initial design space in a topology optimization. They can be defined for the whole structure, for individual properties (components) and materials, or for groups of properties (components) and materials.
The difference between the mass fraction and the volume fraction is that the mass fraction includes the non-design mass in the fraction calculation, whereas the volume fraction only considers the design volume.
Volume fraction = (total volume at current iteration - initial non-design volume)/initial design volume
Mass fraction = total mass at current iteration/initial total mass
If, in addition to the topology optimization, a size and shape optimization is performed, the reference value for the volume fraction (the initial design volume) is not altered by size and shape changes. This can, on occasion, lead to negative values for this response. Therefore, if size and shape optimization is involved, it is recommended to use the Volume responses instead of the Volume Fraction response.
These responses can only be applied to topology design domains. OptiStruct will terminate with an error if this is not the case.
Center of Gravity
This is a global response that may be defined for the whole structure, for individual properties (components) and materials, or for groups of properties (components) and materials.
By default, the center of gravity response is calculated with respect to the basic coordinate system. Refer to PARAM, UCORD to specify a user-defined coordinate system for the calculations.
Moments of Inertia
This is a global response that may be defined for the whole structure, for individual properties (components) and materials, or for groups of properties (components) and materials.
By default, the moment of inertia response is calculated with respect to the basic coordinate system. Refer to PARAM, UCORD to specify a user-defined coordinate system for the calculations.
Weighted Compliance
The weighted compliance is a method used to consider multiple subcases (loadsteps, load cases) in a classical topology optimization. The response is the weighted sum of the compliance of each individual subcase (loadstep, load case).
This is a global response that is defined for the whole structure.
Weighted Reciprocal Eigenvalue (Frequency)
The weighted reciprocal eigenvalue is a method to consider multiple frequencies in a classical topology optimization. The response is the weighted sum of the reciprocal eigenvalues of each individual mode considered in the optimization.
This is done so that increasing the frequencies of the lower modes will have a larger effect on the objective function than increasing the frequencies of the higher modes. If the frequencies of all modes were simply added together, OptiStruct would put more effort into increasing the higher modes than the lower modes. This is a global response that is defined for the whole structure.
Combined Compliance Index
The combined compliance index is a method to consider multiple frequencies and static subcases (loadsteps, load cases) combined in a classical topology optimization. The index is defined as:
This is a global response that is defined for the whole structure.
The normalization factor, , is used to normalize the contributions of compliances and eigenvalues. A typical structural compliance value is of the order of 1.0e4 to 1.0e6. However, a typical inverse eigenvalue is on the order of 1.0e-5. If NORM is not used, the linear static compliance requirements dominate the solution.
The quantity is typically computed using the formula:
Where, is the highest compliance value in all subcases (loadsteps, load cases) and is the lowest eigenvalue included in the index.
In a new design problem, you may not have a close estimate for . If this happens, OptiStruct automatically computes the value based on compliances and eigenvalues computed in the first iteration step.
Bead Discreteness Fraction
This is a global response for topography design domains. This response indicates the amount of shape variation for one or more topography design domains. The response varies in the range 0.0 to 1.0 (0.0 < BEADFRAC < 1.0), where 0.0 indicates that no shape variation has occurred, and 1.0 indicates that the entire topography design domain has assumed the maximum allowed shape variation.
Random Response Analysis
PSD and RMS Responses
PSD displacement, PSD velocity, PSD acceleration, PSD acoustic pressure, PSD stress, PSD strain, RMS displacement, RMS velocity, RMS acceleration, RMS acoustic pressure, RMS stress, and RMS strain responses are available as global, as well as subcase-dependent responses (this information is also available in Subcase Dependent).
Subcase Dependent
Linear Static Analysis
The compliance is calculated using the following relationship:
Where,
or
For a structure with an applied forces subcase, the compliance can be considered a reciprocal measure of the stiffness :
Where, is constant.
For maximum stiffness , the compliance can be minimized.
For a structure with an applied displacements subcase, the compliance can be considered a direct measure of the stiffness :
Where, is constant.
Elements in the Compliance
Compliance can be defined for the whole structure, for individual properties (components) and materials, or for groups of properties (components) and materials. The compliance must be assigned to a linear static subcase (loadstep, load case).
In order to constrain the compliance for a region containing a number of properties (components), the SUM function can be used to sum the compliance of the selected properties (components), otherwise, the constraint is assumed to apply to each individual property (component) within the region. Alternatively, a DRESP2 equation needs to be defined to sum the compliance of these properties (components). This can be avoided by having all properties (components) use the same material and applying the compliance constraint to that material.
Static Displacement
Displacements are the result of a linear static analysis. Nodal displacements can be selected as a response. They can be selected as vector components or as absolute measures. They must be assigned to a linear static subcase.
Static Stress of Homogeneous Material
Different stress types can be defined as responses. They are defined for components, properties, or elements. Element stresses are used, and constraint screening is applied. This is a linear static subcase (loadstep, load case) related response.
Cluster Size of elements to consider for stress response calculation is supported via ATTB field. 32
Corner Stresses are available by setting ATTB=CORNER. Corner stress responses are supported only for Shape, Sizing, and Free-Shape optimization.
Stress Responses for Topology and Free-Size Optimization
Norm-based Approach (Topology and Free-size Optimization)
The Norm-based approach is the default method for handling stress responses for Topology and Free-Size Optimization. This method is used when corresponding stress response RTYPE’s on the DRESP1 Bulk Data Entry are input.
The Response-NORM aggregation is internally used to calculate the stress responses for groups of elements in the model. Solid, shell, bar stresses and solid corner stresses are supported with the Response-Norm aggregation approach (Free-size Optimization is only supported for shell stresses). Refer to NORM Method for more information.
Augmented Lagrange Method (ALM) (Topology Optimization only)
The Augmented Lagrange Method (ALM) is an alternative method for handling stress responses for Topology Optimization. It can be activated using DOPTPRM,ALMTOSTR,1 when DRESP1 Bulk Data Entry is used to specify local stress responses.
ALM is also an alternative method to efficiently solve topology optimization problems with local stress constraints, which is stated in Equation 9.
- Vector of topology design variables
- Objective function
- jth constraint
- Number of local stress constraints
- Total number of constraints
Typically, is equivalent to the number of elements and is a large number. ALM converts the optimization Equation 9 to the following format:
- Element density
- Element von Mises stress
- stress upper bound
- Lagrange multiplier estimator
- Quadratic penalty factor
The Lagrange multiplier estimators are updated as .
In general, the number of local stress constraints is very large. Directly solving Equation 9 is computationally time consuming. By penalizing the stress constraints onto the objective function, the total number of constraints can be significantly reduced. As a result, the optimization problem can be efficiently solved.
The default Stress-norm (P-norm) method continues to efficiently solve Topology Optimization problems with local stress constraints. The ALM 1 is a good alternative for such models.
Global von Mises Stress Response (Topology and Free-size Optimization)
- The definition of stress constraints is limited to a single von Mises permissible stress. The phenomenon of singular topology is pronounced when different materials with different permissible stresses exist in a structure. Singular topology refers to the problem associated with the conditional nature of stress constraints, that is, the stress constraint of an element disappears when the element vanishes. This creates another problem in that a huge number of reduced problems exist with solutions that cannot usually be found by a gradient-based optimizer in the full design space.
- Stress constraints for a partial domain of the structure are not allowed because they often create an ill-posed optimization problem since elimination of the partial domain would remove all stress constraints. Consequently, the stress constraint applies to the entire model when active, including both design and non-design regions, and stress constraint settings must be identical for all DSIZE and DTPL cards.
- The capability has built-in intelligence to filter out artificial stress concentrations around point loads and point boundary conditions. Stress concentrations due to boundary geometry are also filtered to some extent as they can be improved more effectively with local shape optimization.
- Due to the large number of elements with active stress constraints, no element stress report is given in the table of retained constraints in the .out file. The iterative history of the stress state of the model can be viewed in HyperView or HyperMesh.
- Stress constraints do not apply to 1D elements.
- Stress constraints may not be used when enforced displacements are present in the model.
The buckling factor can be constrained for shell topology optimization problems with a base thickness not equal to zero. Constraints on the buckling factor are not allowed in any other cases of topology optimization.
| Composite Stress | Composite Strain | Composite Failure Criterion |
| Frequency Response Stress | Frequency Response Strain | Frequency Response Force |
Grid Point Stress of Homogeneous Material
Different grid point stress types can be defined as responses. They are defined for components, properties, or elements. Grid point stresses are used, and constraint screening is applied. This is currently supported only for Shape, Sizing, and Free-Shape Optimization.
The RTYPE field should be set to GPSTR to activate Grid Point Stress response.
Grid Point Stress Responses for Topology Optimization are available through corresponding GPSTR response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the failure Responses for groups of grids in the model. Refer to NORM Method for more information.
Static Strain of Homogeneous Material
Different strain types can be defined as responses. They are defined for components, properties, or elements. Element strains are used, and constraint screening is applied. It is also not possible to define strain constraints in a topology design space. This is a linear static subcase (loadstep, load case) related response.
Corner Strains are available by setting ATTB=CORNER. Corner strain responses are supported only for Shape, Sizing, and Free-Shape optimization.
Strain Responses for Topology and Free-Size Optimization are available through corresponding Strain response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the Strain Responses for groups of elements in the model. Solid, Shell, Bar Stresses and Solid Corner Strains are supported with the Response-Norm aggregation approach (Free-size optimization is only supported for shell strains). Refer to NORM Method for more information.
Static Stress of Composite Lay-up
Different composite stress types can be defined as responses. They are defined for PCOMP(G), PCOMPP components or elements, or PLY type properties. Ply level results are used, and constraint screening is applied. It is also possible to define composite stress constraints in a topology and/or free-size design space. This is a linear static subcase (loadstep, load case) related response.
Stress Responses for Topology and Free-Size Optimization are available through corresponding Stress response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the Stress Responses for groups of elements in the model. Refer to NORM Method for more information.
Static Strain of Composite Lay-up
Different composite strain types can be defined as responses. They are defined for PCOMP(G), PCOMPP components or elements, or PLY type properties. Ply level results are used, and constraint screening is applied. It is also possible to define composite strain constraints in a topology and/or free-size design space. This is a linear static subcase (loadstep, load case) related response.
Strain Responses for Topology and Free-Size Optimization are available through corresponding Strain response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the Strain Responses for groups of elements in the model. Refer to NORM Method for more information.
Static Failure in a Composite Lay-up
Different composite failure criterion can be defined as responses. They are defined for PCOMP(G) components or elements, or PLY type properties. Ply level results are used, and constraint screening is applied. It is also possible to define composite failure criteria constraints in a topology design space. This is a linear static subcase (loadstep, load case) related response.
Composite Failure Responses for Topology and Free-Size Optimization are available through corresponding Failure response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the failure Responses for groups of elements in the model. Refer to NORM Method for more information.
Static Failure
Different failure criteria can be defined as responses. They are supported for solid and shell elements only. Failure criteria can be defined on the MAT1 or MATT1 entries.
Static Force
Different force types can be defined as responses. They are defined for components, properties, or elements. Constraint screening is applied. It is also not possible to define force constraints in a topology design space. This is a linear static subcase (loadstep, load case) related response.
Single Point Force at a Constrained Grid Point
This response can be defined using the DRESP1 Bulk Data Entry (RTYPE=SPCFORCE). This response is defined for constrained grid points. Constraint screening is applied to this response. This is a linear static subcase (loadstep, load case) related response.
Grid Point Force
This response can be defined using the DRESP1 Bulk Data Entry (RTYPE=GPFORCE). This response defines the contribution to a specific grid point force component from a non-rigid element (which is connected to that grid). Constraint screening is applied to this response. If ATTi specify multiple elements, then multiple responses will be generated; where, each response calculates a specified element's contribution to the grid point force component at the specified grid. This is a linear static subcase (loadstep, load case) related response.
Nodal Electric Potential
Nodal Electric Potential can be used as an internal response when running a linear steady-state electrical conduction analysis with optimization. Nodal Electric Potential response is activated using the RTYPE=ELPOT option. The ATTi field(s) can be used to identify the GRID ID at which the electric potential is calculated for the optimization response.
Global Electric Compliance
Global Electric Compliance can be used as an internal response when running a linear steady-state electrical conduction analysis with optimization. Global Electric Compliance response is activated using the RTYPE=ELCOMP option.
Bore Distortion
Stress Responses for Topology and Free-Size optimization can be defined via the DRESP1 Bulk Data Entry. The Stress Responses are internally aggregated using the Stress-NORM approach to maintain the number of created responses at a reasonable number.
Heat Transfer Analysis
Temperature
Temperatures are the result of a heat transfer analysis and must be assigned to a heat transfer subcase (loadstep, load case). Temperature response cannot be used in composite topology and free-size optimization.
Thermal Compliance
Thermal compliance is calculated using:
- Temperature vector
- Power vector
- Conduction matrix
- Convection matrix
When minimizing thermal compliance, temperatures at grids of flux input are minimized. The optimum structure provides maximum conduction of thermal energy. Since thermal compliance is a smooth convex function, it is typically more efficient to minimize thermal compliance than to perform a min-max of the temperature of the entire structure. During thermal-structural optimization, the temperature field is updated for each iteration. Additionally, for thermal-structural topology optimization, the density design variable affects the conductivity, and the conductivity is also penalized.
Thermal Compliance Response can only be used in Sizing, Shape, Topology, and Free-Size Optimization.
Nodal Flow Pressure (Darcy Flow Analysis)
For a Darcy Flow Analysis nodal flow pressures can be used as an optimization response. The RTYPE should be set as FLOWPRES and the ATTi fields should point to the Grid IDs of the node of interest. This is currently only supported for Topology Optimization with Steady-State Heat Transfer analysis (for which Darcy flow analysis is active).
Normal Modes Analysis
Frequency
Natural frequencies are the result of a normal modes analysis, and must be assigned to the normal modes subcase (loadstep, load case). It is recommended to constrain the frequency for several of the lower modes, not just of the first mode.
- Set the ATTA field on DRESP1 entry equal to the Normal Mode number(s) that you want to use as a response. In this process, you will identify and provide the mode number(s) that are to be optimized.
- You can also source the mode number of the mode with largest modal participation at the peak loading frequency by adding a separate Modal Frequency Response Subcase, in addition to the existing Normal Modes subcase. The ATTA field should identify the number of modes and the ATTi field should be set equal to the subcase ID of the Modal Frequency Response subcase. The Modal Frequency Response Analysis subcase should contain a PEAKOUT entry that identifies peak identification criteria. OptiStruct will internally identify the modes to be optimized based on Modal Frequency Response Analysis, by picking the modes (ATTA) for each peak response which contributes the most to the corresponding response. Therefore, the maximum number of modes identified for the optimization is equal to: number of modes (ATTA) * NPEAK (on PEAKOUT).
Mode Shape
Mode shapes are the result of a normal modes analysis. Mode shapes can be selected as a response. They can be selected as vector components or as absolute measures. They must be assigned to a normal modes subcase.
Linear Buckling Analysis
The buckling factor is the result of a buckling analysis, and must be assigned to a buckling subcase (loadstep, load case).
Buckling Factor
A typical buckling constraint is a lower bound of 1.0, indicating that the structure is not to buckle with the given static load. It is recommended to constrain the buckling factor for several of the lower modes, not just of the first mode.
Linear Transient Analysis
Transient Compliance
Transient compliance, , is defined as:
- Transpose of the time dependent applied force
- Transient displacement
- Final time of the analysis
- Adjoint method for sensitivity calculation is implemented.
- Enforce displacement load (SPCD) is not supported.
- Only MTRAN analysis is support.
- Currently, size, shape and topology optimization are supported.
Transient Displacement
Transient displacement, is defined as:
- Transient displacement
- Applied excitation
- Direct and adjoint method for sensitivity calculation are implemented.
- SPCD is not supported.
- MTRAN and DTRAN analysis are supported.
- Currently, size, shape and topology optimization are supported.
Mean Square of Displacement Difference
Mean Square of Displacement Difference Response, is defined as:
Where, and are the transient displacement of GRID ID and , respectively.
- Adjoint method for sensitivity calculation is implemented.
- Only MTRAN analysis is supported.
- Currently, size, shape and topology optimization are supported.
Frequency Response Function (FRF Analysis)
Frequency Response Displacement
Displacements are the result of a frequency response analysis. Nodal displacements, that is, translational, rotational and normal 1, can be selected as a response. They can be selected as vector components in real/imaginary or magnitude/phase form. They must be assigned to a frequency response subcase (loadstep, load case).
Frequency Response Velocity
Velocities are the result of a frequency response analysis. Nodal velocities, that is, translational, rotational and normal 2, can be selected as a response. They can be selected as vector components in real/imaginary or magnitude/phase form. They must be assigned to a frequency response subcase (loadstep, load case).
Frequency Response Acceleration
Accelerations are the result of a frequency response analysis. Nodal accelerations, that is, translational, rotational and normal 3, can be selected as a response. They can be selected as vector components in real/imaginary or magnitude/phase form. They must be assigned to a frequency response subcase (loadstep, load case).
Frequency Response Stress
Different stress types can be defined as responses. They are defined for components, properties, or elements. Element stresses are not used in real/imaginary or magnitude/phase form, and constraint screening is applied. The von Mises stress for solids and shells can also be defined as direct responses. This is a frequency response subcase (loadstep, load case) related response.
FRF Stress Responses for Topology and Free-Size Optimization are available through corresponding Frequency-response Stress response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the Stress Responses for groups of elements in the model. Solid and Shell FRF Stresses are supported with the Response-Norm aggregation approach (Free-size optimization is only supported with Shell FRF Stresses). Refer to NORM Method for more information.
Frequency Response Strain
Different strain types can be defined as responses. They are defined for components, properties, or elements. Element strains are used in real/imaginary or magnitude/phase form, and constraint screening is applied. The von Mises strain for solids and shells can also be defined as direct responses. This is a frequency response subcase (loadstep, load case) related response.
FRF Strain Responses for Topology and Free-Size Optimization are available through corresponding Frequency-response Strain response RTYPE’s on the DRESP1 Bulk Data Entry.
The Response-NORM aggregation is internally used to calculate the Strain Responses for groups of elements in the model. Solid and Shell FRF Strains are supported with the Response-Norm aggregation approach (Free-size optimization is only supported with Shell FRF Strains). Refer to NORM Method for more information.
Frequency Response Force
Different force types can be defined as responses. They are defined for components, properties, or elements in real/imaginary or magnitude/phase form. Constraint screening is applied. It is also not possible to define force constraints in a topology design space. This is a frequency response subcase (loadstep, load case) related response.
Powerflow
Powerflow can be defined as a Response by setting RTYPE field to FRFLOW. Calculated for a SECTION entry identified via the ATTi field. Constraint screening is applied. It is supported for Topology, Sizing, and Shape Optimization.
Random Response Analysis
PSD and RMS Responses
PSD displacement, PSD velocity, PSD acceleration, PSD acoustic pressure, PSD stress, PSD strain, RMS displacement, RMS velocity, RMS acceleration, RMS acoustic pressure, RMS stress and RMS strain responses are available as global as well as subcase-dependent responses (this information is also available in the Subcase Independent responses section above).
Coupled FRF Analysis on a Fluid-structure Model (Acoustic Analysis)
Acoustic Pressure
Acoustic pressures are the result of a coupled frequency response analysis on a fluid-structure model. This response is available for fluid grids. It must be assigned to a coupled frequency response subcase (loadstep, load case) on a fluid-structure model.
Multibody Dynamics Analysis
Flexible Body Responses
For Multibody Dynamics problems, the Mass, Center of gravity, and Moment of Inertia of one or more flexible bodies are available as responses. This is in addition to other usual structural responses.
MBD Displacement
MBD displacements are the result of a multibody dynamics analysis. They must be assigned to a multibody dynamics subcase (loadstep, load case).
MBD Velocity
MBD velocities are the result of a multibody dynamics analysis. They must be assigned to a multibody dynamics subcase (loadstep, load case).
MBD Acceleration
MBD acceleration are the result of a multibody dynamics analysis. They must be assigned to a multibody dynamics subcase (loadstep, load case).
MBD Force
MBD forces are the result of a multibody dynamics analysis. They must be assigned to a multibody dynamics subcase (loadstep, load case).
MBD Expression
MBD expression responses are the result of a multibody dynamics analysis. They are the result of the evaluation of an expression. They must be assigned to a multibody dynamics subcase (loadstep, load case).
Fatigue
Life/Damage/Factor of Safety
RTYPE=FATIGUE. Life, Damage, and Factor of Safety (FOS) are results of a fatigue analysis. They must be assigned to a Fatigue subcase.
Grid Point based Factor of Safety
Factor of Safety results when RTYPE=GPFAT. They must be assigned to a Fatigue subcase.
Dynamic/Nonlinear Analysis
Equivalent Plastic Strain
Equivalent plastic strain can be used as an internal response when a nonlinear response optimization is run using the equivalent static load method. This is made possible through the use of an approximated correlation between linear strain and plastic strain, which are calculated in the inner and outer loops respectively, of the ESL method.
ESL Velocity
ESL velocity can be used as an internal response, when a nonlinear response optimization is run, using the equivalent static load method. The RTYPE=ESLV option can be used in conjunction with the velocity component value and a GRID ID specification.
Gasket Pressure
Gasket Pressure can be used as an internal response when a nonlinear static analysis with optimization is run. Gasket pressure response is activated using RTYPE=GSKP option. The PTYPE field references PGASK and the ATTi field references the corresponding PGASK ID(s).
Contact Pressure
Contact Pressure can be used as an internal response when a model with contact and optimization is run. Contact pressure response is activated using RTYPE=CNTP option. The PTYPE should be set to CONTACT and the corresponding CONTACT Bulk Data ID(s) can be referenced on the ATTi field. For Shape, Free-Shape, and Sizing optimization, the design variables can be part of the contact region.
Contact Force
Contact Force can be used as an internal response when a model with contact and optimization is run. Contact force response is activated using RTYPE=CNTF option. The PTYPE should be set to CONTACT, the ATTA field should point to the Contact Force item code of interest, and the corresponding CONTACT Bulk Data ID(s) can be referenced on the ATTi field. For Shape, Free-Shape, and Sizing optimization, the design variables can be part of the contact region.
User Responses
Functions
A function response is one that uses a mathematical expression to combine design variables, grid point locations, responses, and/or table entries. Whether the function is subcase (loadstep, load case) related or global, is dependent on the response types used in the equation. Function responses are available via DRESP1, DRESP2, and DRESP3 entries. For DRESP3, the functions are defined using external responses.
External
An external response is one that uses an external user-defined routine to combine design variables, grid point locations, eigenvectors, responses, and/or table entries. Whether the function is subcase (loadstep, load case) related or global is dependent on the response types used in the routine. Refer to External Responses for more information.
Appendix
NORM Method
The NORM method is used to approximately calculate the maximum value of a particular response of all the grids/elements included in a particular response. This is also scaled with the response bounds specified for each grid/element. Therefore, to minimize the maximum response in a particular grid/element set, the resulting NORM value ( ) is internally constrained to a value lower than 1.0.
- Response NORM value
- Number of elements
- Individual response value of grid/element “ "
- Response bound for each grid/element
- Penalty (power) value (default = 6.0)
The Penalty or Power value ( ) can be modified using the parameter DOPTPRM, PNORM. The value = 6.0 is the default and higher values of ( → ) increases the accuracy of the norm function ( → ), which can lead to instability of the optimization run. Values lower than 6 ( → 1) moves the response norm function closer to the average ratio ( → ). The default value is a reasonable approximation of the maximum ratio value and reduces instability.
External Responses
The DRESP3 Bulk Data Entry, in combination with the LOADLIB I/O Option Entry, allows for the definition of responses through user-defined external functions.
The external functions may be written in Compose Open Matrix Language (OML), Fortran, C or a Microsoft Excel workbook. The resulting libraries and files should be accessible by OptiStruct regardless of the coding language, providing that consistent function prototyping is respected, and adequate compiling and linking options are used.
Write External Functions for Optimization Responses
The OptiStruct installation provides
barebone functions for Fortran
(dresp3_barebone.F) and for C (dresp3_barebone.c) with
proper function definition, arguments, and compilation directives.
These files can be used as starting points to write your own functions. Refer to Microsoft Excel Example for information on response definition through a user-defined Microsoft Excel workbook.
integer function myfunct(iparam, rparam, nparam,
iresp, rresp, dresp, nresp, isens
userdata)integer function myfunct(iparam, rparam, nparam,
iresp, rresp, dresp, nresp, isens
userdata)character*32000 userdata
integer nparam, nresp
integer iparam(nparam), iresp(nresp)
double precision param(nparam), rresp(nresp), dresp(nparam,nresp)int myfunct(int* iparam, double* rparam, int* nparam,
int* iresp, double* rresp, double* dresp, int* nresp, int*
isens, char* userdata)- Function names should be written using either all lower-case or all upper-case characters
- Only alphanumeric characters should be used
- Underscore characters are prohibited
- Names cannot be longer than eight characters
Function Return Values
External functions should return 0 or 1 for successful completion, where 1 indicates that a user-defined information message should be output by OptiStruct. External functions should return -1 in case of fatal error, in which case OptiStruct will terminate after outputting a user-defined error message. See below for more information about error and information messages.
Function Arguments
| Argument | Type | Input/Output | Description |
|---|---|---|---|
iparam |
integer (table) | Input | Input parameters types (optional use) |
rparam |
double (table) | Input | Input parameters values |
nparam |
integer | Input | Number of parameters |
iresp |
integer (table) | Input | Output responses requests (optional use) |
rresp |
double (table) | Output | Output responses values |
dresp |
double (table) | Output | Output sensitivity values |
nresp |
integer | Input | Number of responses |
isens |
integer | Input | Sensitivity output flag |
userdata |
string | Input/Output | User data/Error or information message |
nparamis the number of input parameters that were defined on the DRESP3 card.rparam(nparam)contains the values of the input parameters as evaluated by OptiStruct.iparam(nparam)indicates the types of the input parameters as described below.
Parameter values are passed in the exact order in which they were defined on the DRESP3 card, regardless of their type. Using the Parameter Types table is optional, for instance to perform verifications or code-branching.
- Parameter Type
iparamValue- DESVAR
- 1
- DTABLE
- 2
- DGRID/DGRIDB
- 3
- DRESP1
- 4
- DRESP2
- 5
- DRESP1L
- 6
- DRESP2L
- 7
- DVPREL1
- 8
- DVPREL2
- 9
- DVMREL1
- 10
- DVMREL2
- 11
- DVCREL1
- 12
- DVCREL2
- 13
- DVMBRL1
- 14
- DVMBRL2
- 15
- DEIGV
- 16
- DGRIDB
- 18
nrespis the maximum number of responses which the function is able to compute, as defined on the MAXRESP field of the DRESP3 card.rresp(nresp)returns the values of the responses as evaluated by the external function.iresp(nresp)contains the responses requests as described below.The responses requests table indicates which of the available responses are actually needed by OptiStruct. Entries in
iresp(nresp)are flagged as 1 for requested responses and as 0 otherwise. Using that information is optional and allows for saving computational effort by not evaluating responses which OptiStruct does not need.
Userdata String
Upon entering the function, the userdata string contains data as defined in the
USRDATA field of the DRESP3 card. It
provides a convenient mechanism to pass constants or any other relevant information
to the function. There are no restrictions regarding the contents of the string, but
its length must not exceed 32,000 characters.
Upon exiting the function, the string may contain a user-defined error or information message. The updated string is then returned to OptiStruct, where it is printed to the standard output (.out file and/or screen). Here again, the contents of the string are not restricted as long as its length does not exceed 32,000 characters.
The error or information messages may be formatted by using the character "|" as a line-break indicator. Standard C escape sequences are supported, as well. It is advised, but not necessary, to format messages in such a way that each line does not exceed 80 characters, since the same convention is used in OptiStruct output files.
Sensitivity Flag
isens indicates whether sensitivities are requested in the code. It
is recommended to skip the calculation of sensitivities when isens
is turned off. This will avoid unnecessary computations.
Build External Libraries for Optimization Responses
Allows building shared libraries on Windows or Linux.
Refer to Build External Libraries for more information.
External Responses using Altair Compose
Invoking Compose to specify the installation path.
If Altair Compose needs to be invoked during the OptiStruct job in case of external responses (DRESP3), the installation path for Compose must to be specified by the user.
Figure 2. 
- Options field
For further details, refer to -compose in Run Options.
Regarding the implementation of external, user-defined routines using Open Matrix Language (OML), refer to the documentation for Compose OML for writing scripts.
Compose is supported on Windows and Linux operating systems.
External Optimization Responses (DRESP3) Example
Fortran and C-Shared Library
All files referenced here are located in the Altair HyperWorks installation directory under <install_directory>/hwsolvers/demos/optistruct. Copy the files mentioned below to your working directory to run the following examples.
The files
dresp3_simple.F and
dresp3_simple.c contain source code for simple examples
of external functions written in Fortran and C,
respectively. Both functions are named mysum and compute two
responses - the sum of the parameters and the averaged sum of the
parameters.
LOADLIB DRESP3 FLIB dresp3_simple_f.dll
LOADLIB DRESP3 CLIB dresp3_simple_c.dllDRESP3 6 SUMF FLIB MYSUM 1 2
+ DRESP1 2 3
DRESP3 7 AVGF FLIB MYSUM 2 2
+ DRESP1 2 3
DRESP3 8 SUMC CLIB MYSUM 1 2
+ DRESP1 2 3
DRESP3 9 AVGC CLIB MYSUM 2 2
+ DRESP1 2 3DEQATN 1 F(x,y) = x+y
DEQATN 2 F(x,y) = avg(x,y)
DRESP2 4 SUME 1
+ DRESP1 2 3
DRESP2 5 AVGE 2
+ DRESP1 2 3Running this input deck through OptiStruct shows that the Fortran external functions, the C external functions and the internal equations always return the same values, and are updated simultaneously throughout the optimization process.
The file dresp3_advanced.F contains the Fortran source code of the second example, in which you are making use of advanced features of the DRESP3 functionality.
- The USRDATA string is parsed to determine whether stresses or strains are requested, and an error message is returned otherwise.
- The number of parameters is used to determine whether a shell or solid element is treated, and an error message is returned if that number is not equal to 3 or 6.
- An error message is returned if the parameters are not of type DRESP1 or DRESP1L, since stress or strain components are expected.
- Even though the function is able to compute two different responses, only the response(s) actually requested by OptiStruct are computed when the function is called.
- An information message is returned indicating which responses were evaluated.
The input deck dresp3_advanced.fem gives a simple example of problem making use of this external function, for analysis only.
DRESP1 10 SXX2D STRESS ELEM SX1 100
DRESP1 11 SYY2D STRESS ELEM SY1 100
DRESP1 12 SXY2D STRESS ELEM SXY1 100
DRESP1 13 SXX3D STRESS ELEM SXX 50
DRESP1 14 SYY3D STRESS ELEM SYY 50
DRESP1 15 SZZ3D STRESS ELEM SZZ 50
DRESP1 16 SXY3D STRESS ELEM SXY 50
DRESP1 17 SXZ3D STRESS ELEM SXZ 50
DRESP1 18 SYZ3D STRESS ELEM SYZ 50
DRESP1 20 SVM2D-1 STRESS ELEM SVM1 100
DRESP1 21 SMP2D-1 STRESS ELEM SMP1 100
DRESP1 22 SVM3D-1 STRESS ELEM SVM 50
DRESP1 23 SMP3D-1 STRESS ELEM SMP 50DRESP3 30 SVM2D-3 STRLIB GETSTR 1 2
+ DRESP1 10 11 12
+ USRDATA STRESS
DRESP3 31 SMP2D-3 STRLIB GETSTR 2 2
+ SECOND 30
DRESP3 32 SVM3D-3 STRLIB GETSTR 1 2
+ DRESP1 13 14 15 16 17 18
+ USRDATA STRESS
DRESP3 33 SMP3D-3 STRLIB GETSTR 2 2
+ SECOND 32Microsoft Excel Example
Microsoft Excel workbooks can be referenced via the LOADLIB entry to define user-defined responses.
Both Implicit and Explicit options are available and are defined here.
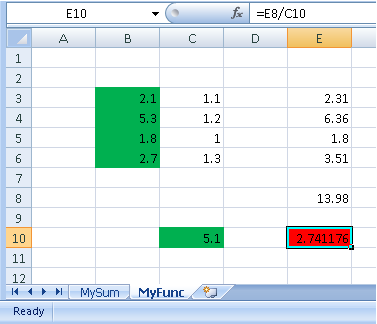
LOADLIB DRESP3 ELIB dresp3_excel.xlsx
DRESP3 10 SUM ELIB MYSUM
+ DRESP1 5 6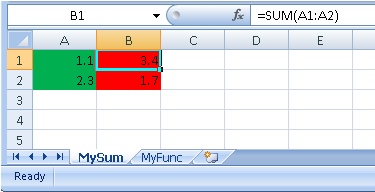
LOADLIB DRESP3 ELIB dresp3_excel.xlsx
DRESP3 20 FUNC ELIB MYFUNC
+ DRESP1 5 6 7 8
+ DESVAR 1
+ CELLIN B3 THRU B6
+ CELLIN C10
+ CELLOUT E10