Réglages des paramètres de la méthode de Newton-Raphson

Paramètres à régler

Les paramètres et stratégies pour la méthode de Newton-Raphson sont réglés automatiquement pour assurer robustesse et performance de la résolution non-linéaire. Il est néanmoins possible pour l'utilisateur d'ajuster ces paramètres, en utilisant l'onglet "Solveurs (systèmes non linéaires)" de la boite d'options de résolution.

Réglages de la méthode de Newton-Raphson

L'utilisateur peut régler les paramètres suivants

• Type de seuil de convergence : trois options sont disponibles, à savoir :

  • Convergence de toutes les variables : toutes les variables du système doivent satisfaire la précision requise ;
  • Convergence globale : la variable présentant la convergence la plus difficile doit satisfaire la précision requise ;
  • Automatique.

  L'option Automatique correspond à l'approche Convergence de toutes les variables dans tous les cas, avec quelques exceptions remarquables, qui sont énumérées ci-dessous :

  • les projets contenant des matériaux hystérétiques (en 2D et 3D) ;
  • lorsque la méthode optimale avec une étape de stabilisation est utilisée pour la relaxation ;
  • les projets Skew avec la stratégie d'initialisation 2D.

  Pour toutes ces exceptions, l'option Automatique correspond plutôt à l'option Convergence globale, car cette approche conduit à des meilleures performances et à une meilleure robustesse.
• Seuil de convergence : précision relative requise pour obtenir la convergence du solveur non linéaire Newton-Raphson. Si les stratégies de relâchement et de durcissement du seuil de convergence sont désactivées, cette valeur est fixe. Sinon, cette valeur est le point de départ pour le critère adaptatif.
• Nombre maximum d'itérations : la valeur par défaut est de 100.
• Le critère de convergence adaptatif repose sur la détection d'une convergence soit facile, soit difficile.

  
  

  

  
  

• Relâchement du seuil : cette stratégie d'adaptation du critère a pour but de faciliter les convergences difficiles. Le déclenchement de l'adaptation du critère est basé sur la décroissance du résidu entre deux itérations de Newton-Raphson consécutives.

  Si la décroissance entre ces deux résidus est inférieure à un pourcentage P (par défaut 10 %), nous considérons une situation de convergence difficile (région rouge sur Figure 1). Si une situation de convergence difficile est détectée, le seuil de convergence est multiplié par un facteur F (par défaut 1.78) pour remonter le critère et faciliter la convergence.

  Le pourcentage P et le facteur F peuvent être modifiés en mode avancé :

  
  
  
  
  

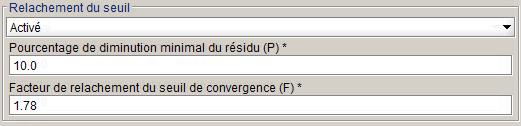
  Cette adaptation de critère est activée par défaut, sauf pour les projets 2D et 3D avec matériaux hystérétiques, les projets non-linéaires utilisant la méthode de relaxation optimale avec une étape de stabilisation et les projets Skew avec l'initialisation 2D.

  Cette stratégie est activée par défaut, sauf :

  • pour les projets contenant des matériaux hystérétiques (en 2D et 3D) ;
  • lorsque la méthode optimale avec une étape de stabilisation est utilisée pour la relaxation ;
  • dans les projets Skew avec la stratégie d'initialisation 2D ;
  • dans les projets 2D contenant des matériaux avec une propriété magnéto-mécanique B(Stress).
• Durcissement du seuil : cette stratégie d'adaptation du critère a pour but de durcir les convergences trop faciles. Le déclenchement de l'adaptation du critère est basé sur la décroissance du résidu entre deux itérations de Newton-Raphson consécutives.

  Si la décroissance entre ces deux résidus est supérieure à un pourcentage P (par défaut 99 %), nous considérons une situation de convergence facile (région jaune sur Figure 1). Si une situation de convergence facile est détectée, le seuil de convergence est divisé par un facteur F (par défaut 3.16) pour descendre ce critère, rendre plus difficile la convergence et assurer la fiabilité des résultats.

  Le pourcentage P et le facteur F peuvent être modifiés en mode avancé :

  
  
  
  
  

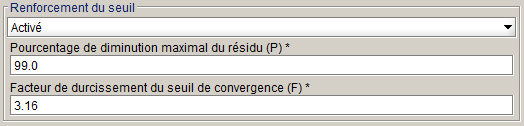
  Cette adaptation de critère est activée par défaut, sauf pour les projets 2D et 3D avec matériaux hystérétiques, les projets non-linéaires utilisant la méthode de relaxation optimale avec une étape de stabilisation et les projets Skew avec l'initialisation 2D.

  Cette stratégie est activée par défaut, sauf :

  • pour les projets contenant des matériaux hystérétiques (en 2D et 3D) ;
  • lorsque la méthode optimale avec une étape de stabilisation est utilisée pour la relaxation ;
  • dans les projets Skew avec la stratégie d'initialisation 2D ;
  • dans les projets 2D contenant des matériaux avec une propriété magnéto-mécanique B(Stress).

Méthode de sous relaxation (3D)

Il existe cinq méthodes pour définir le coefficient de relaxation α de la méthode de Newton Raphson :

• la méthode escalier où le coefficient est déterminé à chaque itération de Newton-Raphson, selon une loi simple en fonction de la précision de Newton-Raphson obtenue
• la méthode fixée, où l'utilisateur entre la valeur du coefficient qui est donc constante pendant la résolution
• la méthode optimale, où le coefficient est déterminé à chaque itération de Newton-Raphson par minimisation du résidu du système non-linéaire à résoudre
• la méthode automatique où le logiciel détermine automatiquement, suivant la formulation, laquelle entre la méthode escalier ou la méthode optimale est utilisée
• la méthode du facteur maximal, où le coefficient est déterminé à chaque itération de Newton-Raphson. C'est le plus grand coefficient permettant de diminuer le résidu du système non-linéaire à résoudre

La méthode automatique est la méthode par défaut. Ces quatre méthodes sont détaillées dans les blocs suivants.

Méthode escalier

Le coefficient de relaxation est déterminé à chaque itération de Newton-Raphson, en fonction de la valeur de la précision ε^i-1 obtenue à l'itération précédente, suivant la loi de variation ci-dessous :

• à la première itération :

  α = 0,5

• aux itérations suivantes :
  • si ε^i-1 ∈[0,1 ; +∞[ : α = 0,5
  • si ε^i-1 ∈[0,01 ; 0,1[ : α = 0,75
  • si ε^i-1 ∈[0 ; 0,01[ : α = 1

Méthode fixée

La valeur du coefficient de relaxation est entrée par l'utilisateur dans l'intervalle ]0 ; 1]. La valeur de ce coefficient est donc constante pendant la résolution.

Méthode optimale

Le coefficient de relaxation est déterminé à chaque itération. Le principe de la méthode consiste à calculer ce coefficient tel que la fonction objectif suivante soit minimale :

$W^i=\sum _{j=1}^n{\left(R_j^i\right)}^2$

où $R_j^i$ est la j-ème composante du résidu R(Xⁱ) à la i-ème itération de Newton-Raphson courante (R(Xⁱ) est un vecteur à n éléments). n est le nombre d'inconnues du système.

La recherche du minimum de la fonction objectif est faite en utilisant une méthode itérative, puisque W ne peut pas s'exprimer de façon explicite en fonction de α. La recherche est faite en calculant les valeurs de Wⁱ pour les valeurs de α = α_k = 1/2^k-1 (α = 1 puis 1/2, 1/4, 1/8...) et en s'arrêtant lorsque Wⁱ_k+1 à l'itération k+1 est plus grand que Wⁱ_k à l'itération précédente k. En effet, au cours des itérations, α = α_k = 1/2^k-1 diminue et Wⁱ_k diminue jusqu'à une certaine itération puis augmente.

Méthode automatique

Flux 3D détermine automatiquement en fonction des formulations présentes dans les régions quelle est la meilleure méthode de relaxation.

Flux 3D choisit automatiquement la méthode optimale, sauf pour les régions qui utilisent une formulation d'impédance de surface en potentiel scalaire magnétique (réduit ou total). Dans ce cas, la méthode escalier sera retenue.

Dans Flux 2D, pour les projets contenant des matériaux avec la propriété magnéto-mécanique B(Stress), la méthode optimale est sélectionnée par la méthode automatique.

Méthode du facteur maximal

Le coefficient de relaxation (α) est calculé à chaque itération de Newton-Raphson. Le principe de cette méthode consiste à rechercher le plus grand coefficient permettant de diminuer le résidu du système non-linéaire à résoudre. Pour cela, le résidu est calculé pour différentes valeurs de α, en essayant en priorité d'augmenter ce coefficient (au maximum à 1) avant de le diminuer uniquement si le résidu du système non linéaire n'a pas diminué par rapport à l'itération de Newton-Raphson précédente.

Plus précisément, l'algorithme fonctionne de la manière suivante : à l'itération i de Newton-Raphson, on démarre avec le coefficient de relaxation α qui a été retenu à l'itération de Newton-Raphson précédente (on démarre à α = 1 si i = 1). On commence par augmenter ce coefficient (α = min (αφ,1), où φ représente le nombre d'or) et on calcule le nouveau résidu du système non linéaire.

• Si ce résidu est inférieur au résidu de l'itération de Newton-Raphson précédente, on continue d'augmenter le coefficient de la même façon, jusqu'à atteindre α = 1 ou un résidu qui n'est plus inférieur à celui de l'itération précédente. On retiendra alors le dernier α (le plus grand) ayant réduit le résidu.
• Si ce résidu est supérieur au résidu de l'itération de Newton-Raphson précédente, on diminue ce coefficient (α = max(α/φ,β), où β est le coefficient de relaxation minimum, déterminé par Flux en fonction du projet). Si le résidu devient alors inférieur au résidu de l'itération précédente, on retient ce coefficient, sinon, on continue de diminuer en suivant la même règle.