Résolution d'un système non-linéaire : méthode de Newton Raphson

Système non linéaire : écriture

Un système non linéaire (n équations / n inconnues) peut s'écrire sous la forme :

[A(X)].[X] = [B] (Equation 1)

où A dépend du vecteur solution X.

Système non linéaire : résolution

La résolution d'un système non linéaire est réalisée à l'aide d'une méthode itérative c'est-à-dire en résolvant une suite de systèmes linéaires dont les solutions convergent vers la solution du problème réel.

Différentes techniques existent, dont la convergence n'est jamais garantie. La méthode utilisée dans Flux est la méthode de Newton Raphson (NR). Elle s'applique à des équations du type f(x) = 0 pour lesquelles on peut calculer la dérivée de f : f'(x).

La méthode de NR est rapidement présentée dans les blocs suivants :

  • à travers une « approche numérique »
  • à travers une « approche graphique » sur un exemple

Méthode de NR : approche numérique

En introduisant : [R(X)] = [A(X)].[X] - [B]

l'équation 1 peut s'écrire : [R(X)] = 0

La méthode de N permet de déterminer itérativement le zéro de cette fonction à partir du développement en série de Taylor.

L'équation à résoudre s'écrit :

où :

  • la matrice dR/dX est la matrice jacobienne
  • le vecteur R(X) est le résidu

A chaque itération, un incrément de solution ΔX est calculé.

Le vecteur solution s'écrit :

Le processus s'arrête lorsque le critère d'arrêt : εi < ε est atteint

où :

  • εi = ||ΔXi+1||/||Xi+1||
  • ε est la précision de Newton-Raphson (fournie par l'utilisateur)

Méthode de NR : approche graphique (1)

La méthode de Newton-Raphson est également dénommée méthode de la tangente. Elle est présentée à travers une « approche graphique », sur un exemple, dans la figure ci-dessous.

Exemple (application Magnéto Statique) :

L'équation résolue par la méthode des éléments finis dans une application magnétostatique s'écrit (modèle vecteur) :

(Equation 2)

où :

  • ν est la réluctivité magnétique du milieu (isotrope)
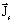  • est la densité de courant source
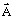  • est le potentiel vecteur (variable d'état / inconnue du système)

Hypothèses :

On peut dire que résoudre l'équation 2 est équivalent à trouver B pour H = Hs sur la caractéristique B(H). Hs est le champ dû au courant source Js.

Approche graphique de la méthode :

On choisit « arbitrairement » une première valeur de B (le zéro par exemple) et on remplace la courbe par sa tangente, on calcule alors facilement (avec l'équation de la droite) une seconde valeur de B. En réitérant la méthode, on s'approche alors de la valeur de B recherchée.

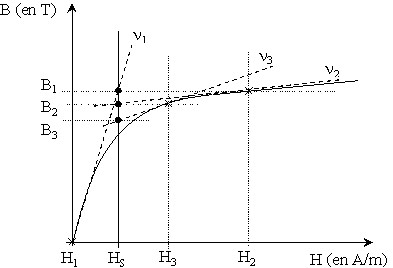
  • 1ère itération (à l'origine) : B = 0 tangente de pente ν1

    calcul de la valeur de B associée à la tangente (B tel que H = Hs) ⇒ B1

  • 2nde itération : B = B1 tangente de pente ν2

    calcul de la valeur de B associée à la tangente (B tel que H = Hs) ⇒ B2

  • 3ème itération : B = B2 tangente de pente ν3

    calcul de la valeur de B associée à la tangente (B tel que H = Hs) ⇒ B3 …