Adaptive solver: error and shutoff criterions

Introduction

Within the framework of an adaptive solver, it is necessary to use:

• An error criterion to detect the meshing areas which are too loose
• A stop signal criterion to set a term to the iterative process in the adaptive solver

Error criterion

In electrostatic, the error criterion is based on the Maxwell-Gauss equation:

In magnetostatics, the error criterion is based on the Maxwell-Ampère equation:

In Steady state AC magnetic, for the conducting region, the error criterion is based on pointing vector. For non conducting region, like in magnetostatics, this is the Maxwell Ampere equation , which is preserved.

From a numerical viewpoint, it should be verified that the accuracy of the equations « weakly » resolved should be satisfactory.

Error criterion in 3D

Adaptive solver detects the locations to refine through an error map. The error criterion depends on the application:

• In Electro Static 3D, the error criterion is based on the Maxwell-Gauss equation:

  

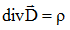
• In Magneto Static 3D, the error criterion is based on the conservation of the magnetic flux density:

  

This error criterion ensures the precision of the equation “weakly” solved.

Shutoff criterion

Currently, there are two stop signal criteria:

• The error threshold based on the energy. This permits the study of the evolution of the energy over a region by calculating the relative energy error from an iteration to another
• The maximum number of iterations of the adaptive solver

How to choose the threshold?

The value of the error threshold is defined either by the user, or automatically by Flux:

• A weak threshold (s = 0.25) is equivalent to a high accuracy
• An average threshold (s = 0.50) is equivalent to an average accuracy
• A strong threshold (s = 0.75) is equivalent to a weak accuracy

Advanced mode

In certain regions, the variation of the electromagnetic field is quasi-inexistent, i.e. null. This is the case of the infinite box, of the perfectly conducting regions and of the inactive regions. In these cases, the Flux software automatically excludes those regions from the adaptive solver.