Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Isotropic / anisotropic materials
Introduction
The studied materials can be isotropic or anisotropic . In other words, the magnetic behavior of the material can be:
- independent of the direction of the applied field (isotropic material)
- dependent on the direction of the applied field (anisotropic material)
These two cases are presented in the sections below.
Isotropic materials
Isotropic materials are characterized by a magnetization law, which is independent of the direction of the applied field.
The ![]() and
and ![]() vectors
are always collinear.
vectors
are always collinear.
The dependence between ![]() and
and ![]() is a scalar
relationship, which is written as: B= μ.H
is a scalar
relationship, which is written as: B= μ.H
Note:
-
for a linear approximation:
μ is a constant ⇒ one can write B= μ.H
-
for a nonlinear approximation:
μ is H dependent ⇒ it is better to write B= μ(H).H
Anisotropic materials
Anisotropic materials are characterized by a magnetization law which is dependent on the direction of the applied field.
The ![]() and
and ![]() vectors
are not collinear.
vectors
are not collinear.
The dependence between ![]() and
and ![]() is a
vector relationship, which is written as:
is a
vector relationship, which is written as: ![]()
where μ is the permeability tensor :
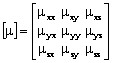
Note:
-
for a linear approximation:
μij is a constant ⇒ one can write
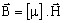
-
for a nonlinear approximation:
μij is H dependent ⇒ it is better to write
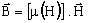
Note on the topic of anisotropy …
Anisotropy can be:
- a crystalline anisotropy, connected to the crystalline structure of the material
- an anisotropy connected to the laminations of magnetic cores, in which case it is called “pseudo-anisotropy”. This form of anisotropy is taken into account through a specific region called « Laminated magnetic non conducting region » (see the chapter Physics: Principles )
Crystalline anisotropy (in the sheet plane)
The models that permit the taking into consideration of the crystalline anisotropy are those models focused on the 2D anisotropy (i.e. only in the sheet plane ).
These models mainly observe the measured magnetic characteristics of the sheets in their main directions, the direction of lamination DL, and the transversal direction DT .
The following models can be cited from the Nahil HIHAT thesis:
- separation of the axes model NIYS75
- model of the two axes HLN84
- elliptical model and elliptical model with axes rotation DNP83
- empirical anisotropic models …
Preferred directions of a sheet:
- DL: direction of lamination
- DT: transversal direction
- DN: normal direction
Bibliography
Complementary information on the modelling of anisotropic magnetic materials is available in the following documents:
- “Quasi 3D Models for the Analysis of Structures Presenting a 3D Anisotropy”- thesis of Nabil HIHAT – 2010Université Lille Nord de France – UArtois
- “Anisotropic and nonlinear laws of magnetization: modelling and experimental validation”thesis of Thierry PERA – 1994INPG ()
- “Contribution to the bi-dimensional and three-dimensional modelling of anisotropy phenomena in 3-phase transformers” thesis of Jean Marc DEDULLE – 1990INPG ()
References regarding semi-analytical 2D models (plane of the sheet) :
-
NIYS75 T. Nakata, Y. Ishihara, K. Yamada et A. Sasano :
Non-linear analysis of rotating flux in the t-joint of a three-phase, three-limbed transformer core.
In proceedings of Soft Magnetic Materials 2 Conference, pages 57-62. 1975.
-
HLN84 D. Huttenloher, H.W. Lorenzen et D. Nusheler :
Investigation of the importance of the anisotropy of cold rolled electrical steel sheet. IEEE Transactions on Magnetics , 20(5):1968 -1970, 1984.
-
DNP83 A. Di Napoli et R. Paggi :
A model of anisotropic grain-oriented steel.
IEEE Transactions on Magnetics , 19(4):1557-1561, 1983.
Difficulties in modeling magnetic anisotropy
For an anisotropic material, permeability appears as tensor quantity with each of the components depending on the applied field.
The vector relationship B(H) is therefore written in the form of 3 families of curves:
- Bx (Hx, Hy, Hz)
- By (Hx, Hy, Hz)
- Bz (Hx, Hy, Hz)
The description of this type of curve at the experimental level is quite delicate, as one must be able to measure simultaneously both the magnitude and direction of magnetic flux density as a function of the field H.
Generally, we limit ourselves to measurements in the directions where the magnetic field strength H and the magnetic flux density B are parallel.
Supposing that these characteristics exist, one must then be able to input them into the software, and the software must be able to carry out the necessary interpolations during the numerical calculations.
For all these various reasons, at the present time:
- there are simplified models, but whose validity domains are limited
- the nonlinear anisotropic models require more research
Simplified models
Generally, simplified models are based on a separation of the phenomena along the main axes of the material.
The methodology consists of expressing the vector relationship B(H) starting from three main directions with respect to the modeled material and achieving the most representative interpolation (linear interpolation, elliptical, …).
Each class of materials must be examined in a different manner (soft magnetic materials, permanent magnets).
… in Flux: linear model
The simplified model provided in Flux for linear model incorporates the separation of axes with linear interpolation .
The vector dependence between ![]() and
and ![]() which is written as:
which is written as: ![]() can therefore be expressed in the form of three curves: Bx(Hx), By(Hy) and Bz (H z ).
The correspondent axis Ox, Oy and Oz are called the main axis of magnetization.
can therefore be expressed in the form of three curves: Bx(Hx), By(Hy) and Bz (H z ).
The correspondent axis Ox, Oy and Oz are called the main axis of magnetization.
The permeability tensor is written: 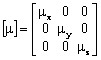
This purely mathematical formalism is very simple and convenient at the level of resolution. It renders the fact that at the microscopic level the magnetic flux density and the magnetic field strength are collinear on three main directions: privileged direction, transversal direction and a third direction.
In case of anisotropic laminations, these directions might be the direction of the sheet lamination, the transversal direction (in the plane of the sheet) and the orthogonal direction, normal to the sheet.
For a permanent magnet, these directions will be the magnetization direction, as well as the two directions perpendicular to the first one.
Bibliography
Complementary information on the modeling of anisotropic magnetic materials is available in the following documents:
- “Lois d'aimantation anisotropes et non linéaires : modélisation et validation expérimentale”thesis of Thierry PERA – 1994INPG (Anisotropic and nonlinear laws of magnetization: modeling and experimental validation)
- “Contribution à la modélisation bidimensionnelle et tridimensionnelle des phénomènes d'anisotropie dans les transformateurs triphasés” thesis of Jean Marc DEDULLE – 1990INPG (Contribution to the bi-dimensional and three-dimensional modeling of anisotropy phenomena in 3-phase transformers)
… in Flux : non linear model
The model used in Flux to take into consideration the linear anisotropic materials cannot be generalized for the non linear case.
A new model with elliptical interpolation has therefore been created for the non linear materials (in 2D). It is not presented in detail in this document, but the bibliographic references are given in the section below.
Biroet al., 2010 Biro, O., Außerhoger, S., Preis, K., and Chen, Y. (2010). A modified elliptic model of anisotropy in nonlinear magnetic materials. COMPEL : The Internationnal Journal for Computation and Mathematics in Electrical and Electronic Engineering , 29(6):1482 – 1492.
Dedulle et al., 1990 Dedulle, J.-M., Meunier, G., Foggia, A., Sabonnadiere, J.-C., and Shen, D. (1990). Magnetic fields in nonlinear anisotropic grain-oriented iron-sheet. IEEE Transactions on Magnetics , 36(2):524 – 527.
Napoli and Paggi, 1983 Napoli, A. D. and Paggi, R. (1983). A model of anisotropic grain-oriented steel. IEEE Transactions on Magnetics , 19(4):1557 – 1561.