Introduction / examples

Definition

A system is said to be nonlinear when one of the properties of the system is a function of the variable that is an unknown of the system. Two examples are presented in the following paragraph.

Example 1 (thermal application)

The differential equation solved using finite element method in a Steady State Thermal application is the following:

where:

  • [k] is the tensor of thermal conductivity
  • q is the volume density of power of the heat source
  • T is the temperature, respectively the state variable, i.e. the unknown of the system.

If the thermal conductivity k is a function of the temperature T, the system is a nonlinear system.

Example 2 (magnetic application)

The differential equation solved using the finite element method in a Magneto Static application (with the scalar model) can be written:

where:

  • [μ] is the tensor of magnetic permeability in the computation domain
  • ϕ is a magnetic scalar potential, respectively the state variable
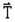  • is a term corresponding to sources (imposed field source or electric vector potential).

If the magnetic permeability μ is a function of the magnetic field H, respectively of the state variable ϕ, the system is a nonlinear system.

Example 2 prime (magnetic application)

The differential equation solved using finite element method in a Magneto Static application (with vector model) can be written:

where:

  • [ν] is the tensor of magnetic reluctivity of the computation domain
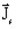  • is the density of current source
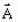  • is the vector potential, respectively the state variable, i.e. the unknown of the system

If the magnetic reluctivity ν is a function of the magnetic flux density B, respectively of the state variable A, the system is a nonlinear system.

Different possibilities

A system is called nonlinear in Flux applications when:

  • behavior laws of materials (constitutive equations) are nonlinear

    • B(H) nonlinear law:

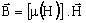
      (magnetic permeability μ function of the magnetic field H)

    • J(E) nonlinear law:

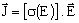
      (electric conductivity σ function of the electric field E)

    • D(E) nonlinear law:

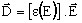
      (electric permitttivity ε function of the electric field E)

  • a thermal property depends on temperature…
    • thermal conductivity k function of T
    • volume heat capacity function of T
    • thermal exchange coefficients function of T

... in Flux

A brief description of the models proposed in Flux is presented in the two tables below:
  • Models for the behavior laws (electromagnetic properties)
    B(H) J(E) D(E)
    Soft materials Hard materials
    Linear Linear Linear Constant resistivity Linear
    Linear complex

    Linear complex

    Linear with losses
    Nonlinear

    Saturation:

    • analytic
    • analytic + knee adjustment
    • spline

    Rayleigh

    Demagnetization:

    • analytic
    • analytic + knee adjustment
    • spline
    		 Superconductor
  • Models for thermal properties
    k(T) ρCp(T)
    constant constant
    linear function of T linear function of T
    exponential function of T exponential function of T
    sum of a Gaussian function of T and a constant
    sum of a Gaussian function of T and an exponential function of T

The models presented above are described in chapter Materials: principles.