Different criterions for different applications
Introduction
All criterions are not adapted for all applications or all regions.
In most cases, an error criterion that is not relevant for an application is not be available. For instance the thermal error criterion is available for thermal applications only. Nevertheless, it has not been always possible to filter enough so that all error criterions are relevant for all situations.
The next tables indicate which criterion is relevant for which application and region.
2D criterions versus region type
The next table indicates which criterion is relevant for which region for the 2D magnetic applications:
| Error criterion | Equation | Massive conductor | Meshed coils | Magnetic non conducting | Air or vacuum |
|---|---|---|---|---|---|
| Power balance |  |
 |
 |
|
|
| Magnetic vorticity conservation | rotH = J | |
|
|
|
| Magnetic co-energy gradient |
|
|
|
|
|
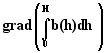
3D criterions versus region type
The next table indicates which criterion is relevant for which region for the 3D magnetic applications:
| Error criterion | Equation | Massive conductor | Meshed coils | Magnetic non conducting | Air or vacuum |
|---|---|---|---|---|---|
| Current conservation | divJ = 0 | |
|
|
|
| Magnetic induction conservation | divB = 0 | |
|
|
|
| Power balance | |
|
|
|
|
| Magnetic co-energy gradient |
|
|
|
|
|
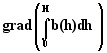
Non relevant error criterion
When an error criterion is not relevant for a region type (for instance the current balance in air region), an error message is return in the dialog windows to indicate it is not relevant for the selected region.
Magneto-thermal error criterion
The error criterion provided for the magneto-thermal applications are the same than the one for the magnetic application, but with the thermal flux conservation in more.
Error criterion for the other applications
The other criterions provided for all the other application (electrostatic, stady states AC electric, electric conduction, thermal applications) are unique and relevant for all the region of the application.
Error criterion and mesh order
Error criterions are not fully adapted to provide precise results for a first order mesh. They can give global indications, but the error is not decreasing whith a more dense mesh.
Outlook
Error criterions that are provided open the way toward an auto-adaptive mesh solver. We will then imagine that with this next development, a simulation design process where you would not have to define the mesh by yourself and getting results precise enough.