Theoretical aspect of the method

Introduction

This section introduces some principle to explain on what is based the computation for the error criterion.

Method principle

Flux provides 2 different methods that can be complementary to determine the error of a solution.

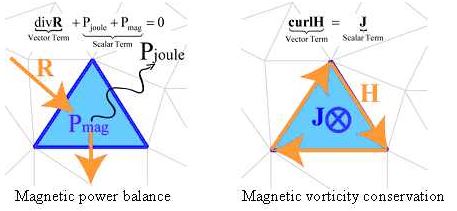
A first method is based on the conservation law of physical quantities. Quantities such as the energy conservation, the conservation of the magnetic flux density or the conservation of the heat flux.

A second computation method is based on the analysis of the local variation (gradient) of the co-energy. This last method is less physics meaningful and supposes that the more the energy quantities are varying, the greater the error.

Whatever the chosen method, this computation consists in the local evaluation of the equation for each finite element. This allows also visualising area where the error is the most important. It gives an error balance for each region to give element of comparison for different solutions.

Conservation law for Flux

In electromagnetism, many conservation laws have to be verified. For Flux, these equations are:

  • Current conservation law:

div(J) = 0

with J the current density vector.

  • Magnetic induction conservation law:

div(B) = 0

with B the magnetic induction vector.

  • Maxwell-Gauss equation:

div(D) = 𝜌

with D the electric induction density vector, and 𝜌 the volume charge density.

  • Power balance equation:

with E×H , the electromagnetic power density vector, J•E the volume Joule losses density and H ∙ ∂ B ∂ t the volume magnetic power density.

  • Thermal flux conservation:

div(Jt) = q

with Jt the thermal flux density vector and q the heat source volume density.

Co-energy variation equations

The 2 criteria: gradient of the magnetic co-energy and of the electric co-energy are based on the study of the variation (gradient) of the co-energy.

  • Gradient of the magnetic co-energy:

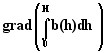
  • Gradient of the electric co-energy:

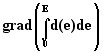
References

For more details have a look to the following paper:

Rondot L. , Mazauric V., Wendling P., « An Energy-Compliant Magnetodynamic Error Criterion for Eddy-Current Calculations », IEEE Trans. Magn., June 2010, Vol. 46 issue 6 p. 2353 - 2356