直交異方性材料のプロパティの定義
直交異方性の材料特性を工学定数で定義します。
形式
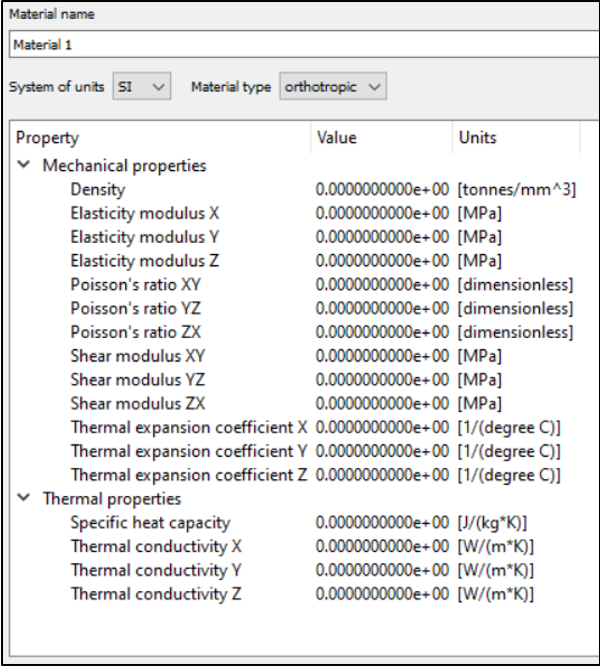
例
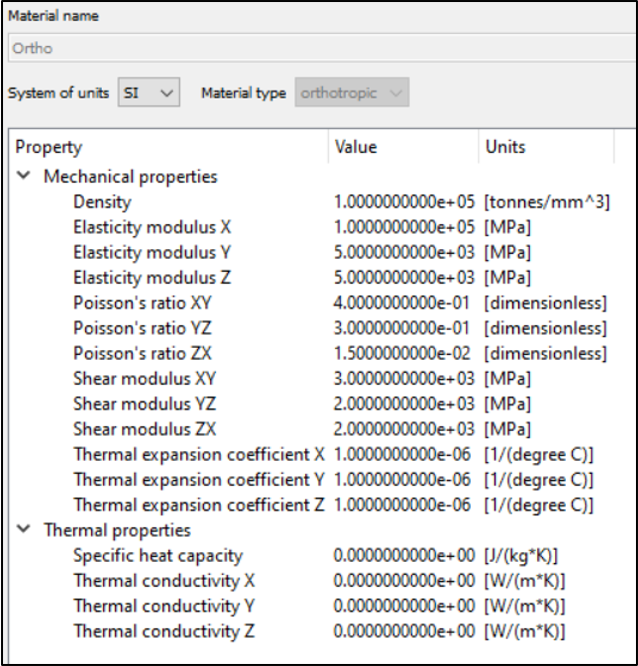
コメント
- 直交異方性材料は、その材料特性において、相互に垂直な3つの対称面を持ちます。直交性線形弾性材料の応力-歪み関係は、以下のようになります。コンプライアンス行列 は以下のように与えられます:
Figure 3. 
Figure 4. 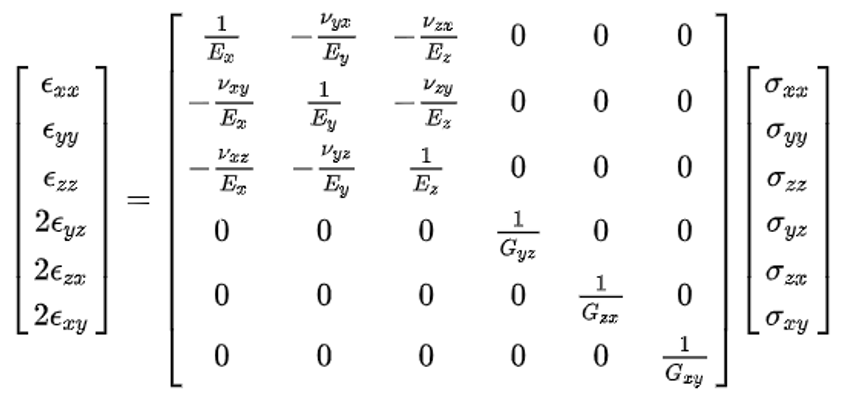
Figure 5. 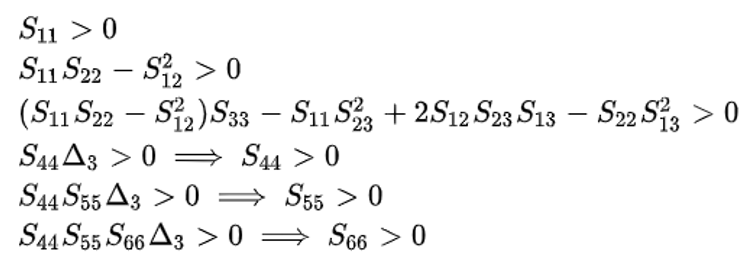
Figure 6. 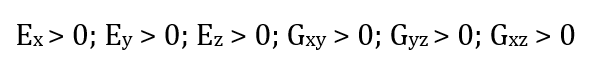
上記の条件を満たさない場合は、エラーとなります。Figure 7. 
- 熱解析に必要な場合は、熱膨張係数(X、Y、Zに沿った)、熱プロパティを与えます。