Home
Verification Problems
Solved verification models.
Non-linear
SS-V: 5040 Residual Deformations in an Axially Loaded Plastic Bar
Test No. VNL05 Find residual deformations in a bar axially loaded beyond plasticity.

Welcome
What's New
View new features for SimSolid 2024.1.
Get Started
Learn the basics and discover the workspace.
Tutorials
Discover SimSolid functionality with interactive tutorials.
Interface with External Products
Interfaces that support SimSolid output file format.
Geometry
Information about treatment and properties of geometric entities in SimSolid.
Assembly
Summary of available functionality for defining the properties and behavior of parts in the model.
Connections
Connections are used to define the association of different regions of interest between parts in an assembly.
Create Analysis
Create an analysis for your project.
Boundary Conditions
Boundary Conditions available for SimSolid.
Post Processing
Run analyses and view a variety of results in SimSolid.
Design Study
Design studies allow you to quickly evaluate and compare the structural performance from different design scenarios.
Verification Problems
Solved verification models.
- Introduction
  The purpose and format of the SimSolid verification problems document.
- Access the Model Files
  Learn how to access and download required model files.
- Static Analysis
- Modal Analysis
- Thermal Analysis
- Thermal Loading
- Non-linear
  - SS-V: 5000 Coupled Analysis - Bimetallic Beam Under Thermal Load
    Test No. VNL01 Find temperature at the material interface and maximum deflection of the beam.
  - SS-V: 5010 Z-Shaped Cantilever
    Test No. VNL02 Find vertical dsiplacements of a Z-shaped cantilever beam under transverse loads of varying magnitude.
  - SS-V: 5020 Lateral Buckling of a Right Angle Frame
    Test No. VNL03 Perform analysis of buckling and post-buckling of a thin-walled frame-like structure in the shape of right angle.
  - SS-V: 5030 Reactions at the Ends of Axially Loaded Plastic Bar
    Test No. VNL04 Find reactions at the fixed ends and maximum displacement of a bar axially loaded beyond plasticity.
  - SS-V: 5040 Residual Deformations in an Axially Loaded Plastic Bar
    Test No. VNL05 Find residual deformations in a bar axially loaded beyond plasticity.
  - SS-V: 5060 Separate Beams
    Test No. VNL07 Find total or partial beam separation/slippage depending on the applied loads.
  - SS-V: 5070 Pinched Hemispherical Shell
    Test No. VNL08 Find displacements of a hemispherical shell loaded with inward and outward concentrated forces.
  - SS-V: 5080 Rigid Punch Plasticity
    Test No. VNL09 Find out reactions at the punch pressed on large block for perfectly plastic and isotropic hardening materials.
  - SS-V: 5090 Bushing Stiffness
    Test No. VNL10 Find the rotation of cylinder subjected to a moment of 10 N-m along its length.
- Dynamics
- Fatigue
- Composites
Frequently Asked Questions
This section provides quick responses to typical and frequently asked questions regarding

SS-V: 5040 Residual Deformations in an Axially Loaded Plastic Bar

Test No. VNL05 Find residual deformations in a bar axially loaded beyond plasticity.

Definition

Figure 1.

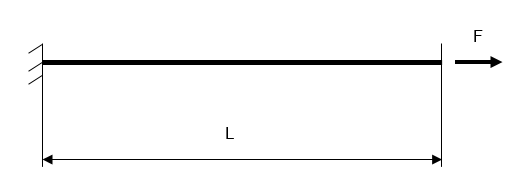
Bar dimensions are 10 x 10 x 200 mm. Strain-stress curve of the bar material is defined by the power law:

σ = K ε^{n}

Where,

$K$

Strength coefficient.

$n$

Must be in the range [0,1].

$n$ =0: Material is perfectly plastic.
$n$ =1: Material is elastic.

The left end of the bar is clamped and the right end is loaded with force F.

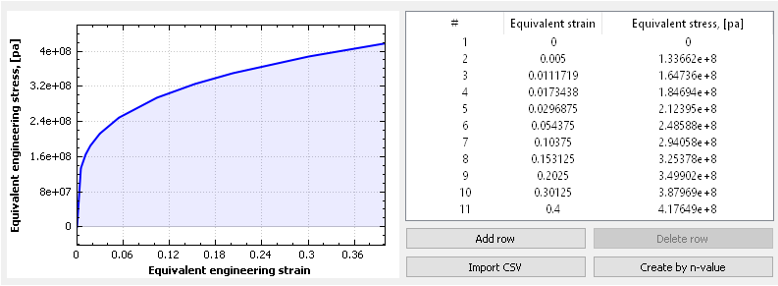
The material properties are:

Properties: Value
$K$: 530 MPa
$n$: 0.26
Poisson's Ratio: 0

Figure 2. Corresponded strain-stress curve

Note: Elasticity modulus defined by the first two points of the strain-stress curve is E=2.67324e+10 Pa.

The study was performed for the following load F values: 20000 N, 25000 N, and 30000 N

Reference Solution

One-dimensional analytical reference solution is described here.

At strain $ε$ and stress $σ$ , the residual strain is:

ε r = ε - ε e = (\frac{σ}{K}) \frac{1}{n} - \frac{σ}{E} = (\frac{F}{(K * A)}) \frac{1}{n} - (\frac{F}{(E * A)})

Where,

$ε$: Total strain in the bar.
$ε e$: Elastic component of the total strain.
$ε r$: Residual strain.
$A$: Bar cross-section area.

Then residual displacement at the right end of the bar.

U r = \int_{0}^{L} (\sqrt[n]{\frac{F}{K * A}} - F / (E * A)) d x

Results

The bar was modeled as a 3D solid. The left end of the solid was fixed and the right end loaded with axial force (Figure 3).

Figure 3.

The following table summarizes the residual deformations results.


Force F [N]	SOL Reference, Residual Displacement [mm]	SimSolid, Residual Displacement [mm]	% Difference
20000	3.22	3.3	2.48%
25000	9.16	9.23	0.76%
30000	19.077	20.2	5.89%