/FUNCT_SMOOTH

Block Format Keyword Defines a smoothstep analytic function to be used with loads.

Format


(1)	(3)	(5)	(7)
/FUNCT_SMOOTH/`fct_ID`
`fct_title`
`Ascalex`	`Fscaley`	`Ashiftx`	`Fshifty`
`X`₁	`Y`₁
`X`₂	`Y`₂
etc.	etc.
`X`_N	`Y`_N

Definition


Field	Contents	SI Unit Example
`fct_ID`	Function identifier. (Integer, maximum 10 digits)
`fct_title`	Function title. (Character, maximum 100 characters)
`Ascalex`	Abscissa scale factor. Default = 1.0 (Real)
`Fscaley`	Ordinate scale factor. Default = 1.0 (Real)
`Ashiftx`	Abscissa shift value. Default = 0.0 (Real)
`Fshifty`	Ordinate shift value. Default = 0.0 (Real)
`X`₁	First abscissa for the function definition. Default = 0 (Real)
`Y`₁	First ordinate for the function definition. Default = 0 (Real)
`X`₂	Second abscissa for the function definition. (Real)
`Y`₂	Second ordinate for the function definition. (Real)
`X`_N	(Optional) N^th abscissa point. (Real)
`Y`_N	(Optional) N^th ordinate point. (Real)

Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT_SMOOTH/1
Displacement
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#            Ascalex             Fscaley             Ashiftx             Fshifty   

#                  X                   Y  
                   0                   0                                                            
                  .2                  60				   
                  .4                  20				   
                  .5                  70				   
                  .6                  70				   
                  .8                 0.0				   
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA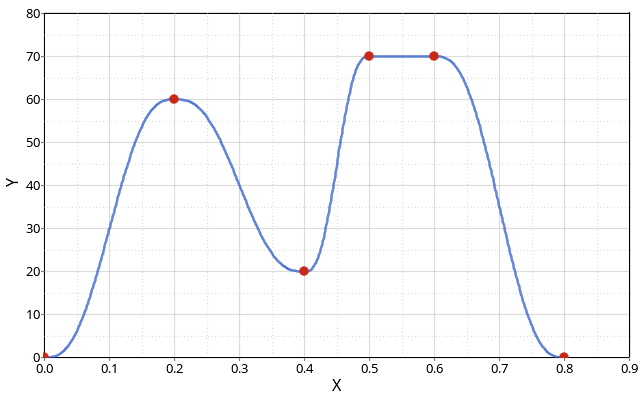

Comments

Points 1 and 2 are required.
A function and a table cannot share the same identifier.
This function can be used with these options:
/IMPDISP, /IMPDISP/FGEO, /IMPFLUX, /IMPTEMP, /IMPVEL, /IMPVEL/FGEO, /IMPVEL/LAGMUL, /IMPACC, /CLOAD, /PLOAD and /GRAV.
For an abscissa smaller than X₁, the ordinate value is Y₁.
For an abscissa larger than X_N, the ordinate value is Y_N.
The function is scaled first and shifted afterwards, as:
$X_{n e w} = X_{o l d} \cdot A s c a l e_{x} + A s h i f t_{x}$
$Y_{n e w} = Y_{o l d} \cdot F s c a l e_{y} + F s h i f t_{y}$
Where, $X_{o l d}$ and $Y_{o l d}$ are values from the function.
The ordinate is calculated for each time step which results in a smooth function.
The function is calculated for using two consecutive input data points $i$ and $i + 1$ as:
$\begin{array}{l} If x \leq X_{1} then y = Y_{1} \\ {If X}_{1} < x < X_{N} then y = y_{i} + (y_{i + 1} - y_{i}) d^{3} (10 - 15 d + 6 d^{2}) \\ where, d = \frac{x - x_{i}}{x_{i + 1} - x_{i}} \\ If x \geq X_{N} then y = Y_{N} \end{array}$