OS-E: 0850 V-Bracket using RADOPT

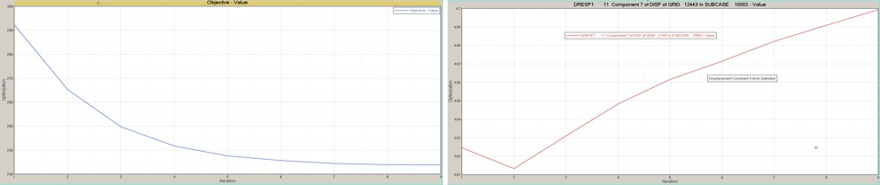
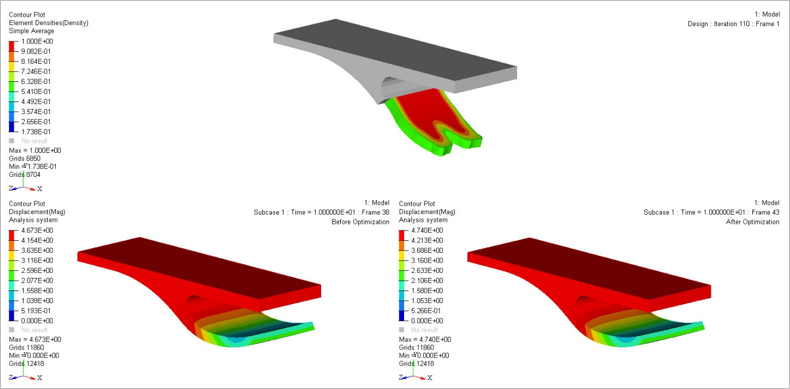
Demonstrates topology optimization of a V-bracket with RADOPT technique, using OptiStruct. RADOPT is Radioss optimization using OptiStruct. The equivalent static load method (ESLM) is used to perform the optimization run here.

Figure 1. FE Model


Model Files

Before you begin, copy the file(s) used in this example to your working directory.

Model Description

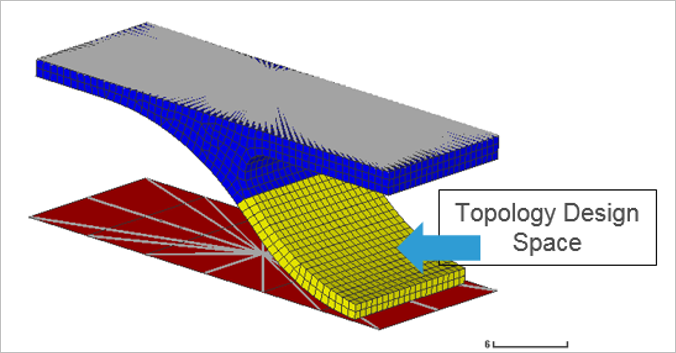
Conduct a topology optimization of the V-bracket which is undergoing a compression loading (force applied in negative Y-direction), and the design space (yellow) in Figure 1.
FE Model
Elements Types
HEXA
RBE2
The linear material properties are:
MAT1
Young’s Modulus
2.1E5 MPa
Poisson's Ratio
0.3
Density
7.9E-9

Results

Based upon these findings, a topology optimization, the Design Objective and Design Constraint satisfied (Figure 2) and also design change on the V-bracket in Figure 3 are found.
Figure 2. Design Objective and Design Constraint


Figure 3. Element Density Results