OS-E: 0897 Multi-Material Topology Optimization of Automotive Chassis

Multi-Material Optimization (MMO) can be used in applications that require optimizing the parts of different materials. This method offers an initial concept-level look at material placement within the structure, where multiple materials can be evaluated.

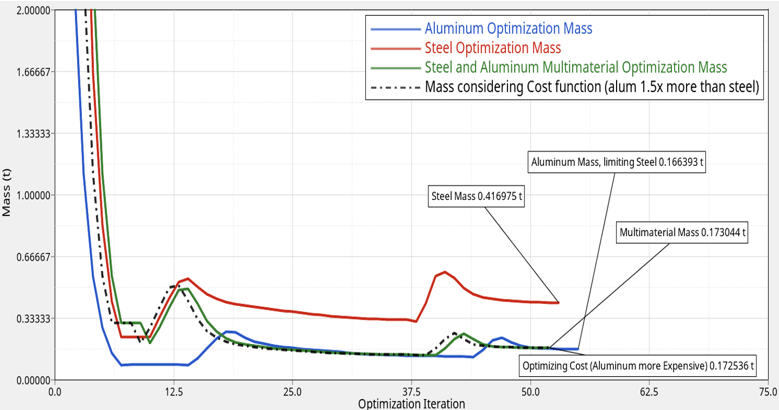
The relationship between the mass savings, stiffness, and relative cost to manufacture the material can be included in the optimization formulation.

Without a consistent formulation, optimization would favor the lightest or stiffest material (steel or aluminum) but competing requirements can guide the design.

Multi-material optimization can be used when information outside of the structural performance is known that would influence total production costs, such as the relative price of different materials, and the relative volume production of each of them.

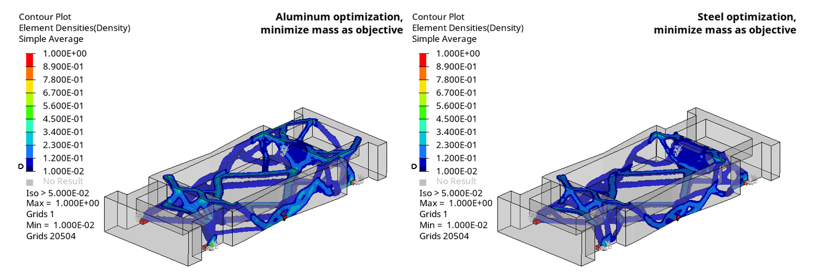
Consideration to include manufacturing constraints can help guide the resulting structures to be better produced by traditional methods.
  • Case 1:
    Objective: Topology optimization considering steel and aluminum individually
    Steel optimization
    Higher mass, less material to meet stiffness requirements.
    Aluminum
    Less mass, more material to meet stiffness requirements.
    Cost of aluminum may be higher.
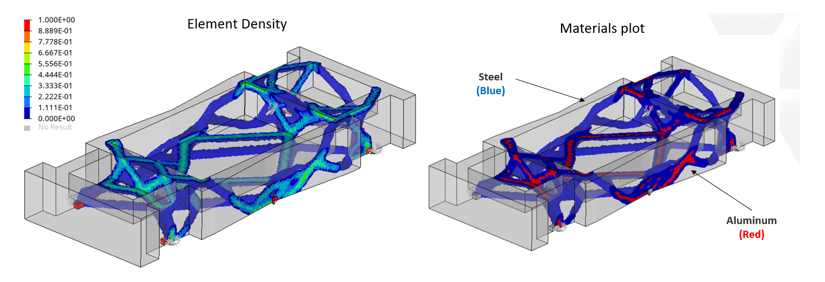
  • Case 2:

    Topology optimization considering multiple materials (steel + aluminum)

    Objective: Minimize the total mass of steel and aluminum material in the structure.

    Resulting design meets the stiffness requirement while removing material where unnecessary.

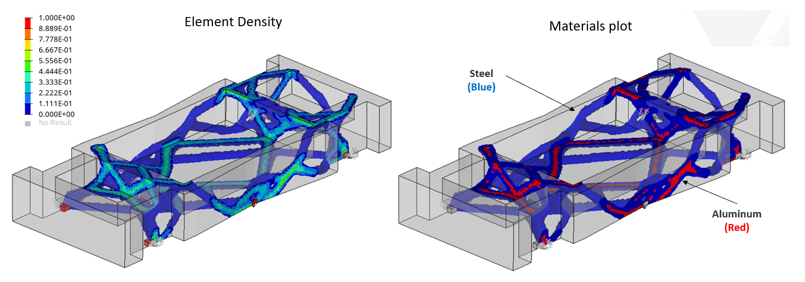
  • Case 3:

    Topology optimization considering multiple materials and minimizing relative cost.

    Objective: Minimize cost function as a function of mass f ( x , y ) = x + 1.5 ∗ y MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm aabaGaamiEaiaacYcacaWG5baacaGLOaGaayzkaaGaeyypa0JaamiE aiabgUcaRiaaigdacaGGUaGaaGynaiabgEHiQiaadMhaaaa@4213@ , where aluminum costs 50% more than steel.

    Since the cost of aluminum is higher than steel, by taking this into account, look at where to place the material.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

Model Description

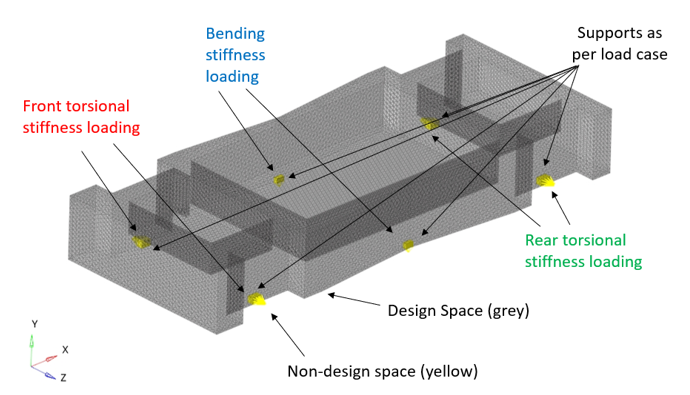
In this example, Multi-Material Topology Optimization is performed on the automotive chassis (aluminum + steel) model with 3 different objectives to fulfill.


Figure 1. Chassis Model with Constraints and Loading Conditions
  • Unit loads for three scenarios: bending, front torsional stiffness, and rear torsional stiffness
  • Displacement constraints applied at all the loading locations based on baseline analysis
  • Symmetry constraint at the mid-plane
FE Model
Chassis body
CTETRA
Connectors
Rigid elements (RBE2)
Linear Material Properties (MAT1)
Aluminum
Young's modulus
7E+04 MPa
Poisson's ratio
0.33
Density
2.7E-09 ton/mm3
Steel
Young's modulus
1.95E+05 MPa
Poisson's ratio
0.29
Density
9E-09 ton/mm3

Results



Figure 2. Case 1 Topology Optimization Results


Figure 3. Case 2 Topology Optimization Results


Figure 4. Case 3 Topology Optimization Results


Figure 5. Results Comparison. tracking the mass over the optimization iterations for different scenarios