Pretensioned Bolt Analysis
Many engineering assemblies are put together using bolts, which are usually pretensioned before application of working loads.
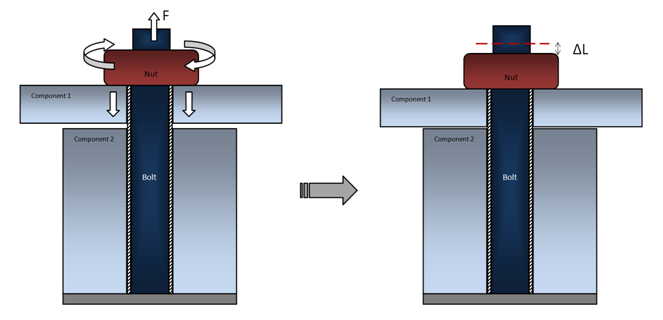
In Step 1, upon preliminary assembly of the structure, the nuts on respective bolts are tightened, usually by applying specified torque (which translates into specified tension force according to the pitch of the thread).
As the result, the working part of the bolt becomes shorter by a distance . This distance depends upon the applied force, the compliance of the bolt and of the assembly being pretensioned.
- Pretensioning shortens the working part of the bolt by removing a certain length of the bolt from the active structure (in reality this segment slides through the nut, yet the net effect is the shortening of the working length of the bolt). Since the bolt stretches, there is a smaller effective length of the bolt material to span the distance from the bolt mount to the nut.
- Calculation of each bolt's shortening , due to applied forces , requires FEA solution of the entire model with the pretensioning forces applied. This is because the amount of nut movement due to given force depends on the compliance of the bolts, of the assembly being bolted and is also affected by cross-interaction between multiple bolts being pretensioned.
At the end of Step 1, the amount of shortening for each bolt is established and "locked", simply by leaving the nuts at the position that they reached during the pretensioning step.
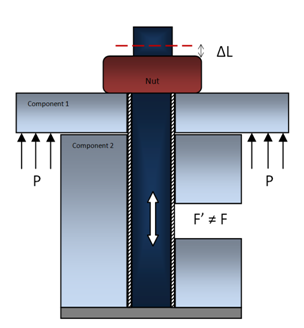
Application Variations
In practice, there may be variations of the application of pretensioning loads and more complex pretensioning sequences than that presented above. For example:
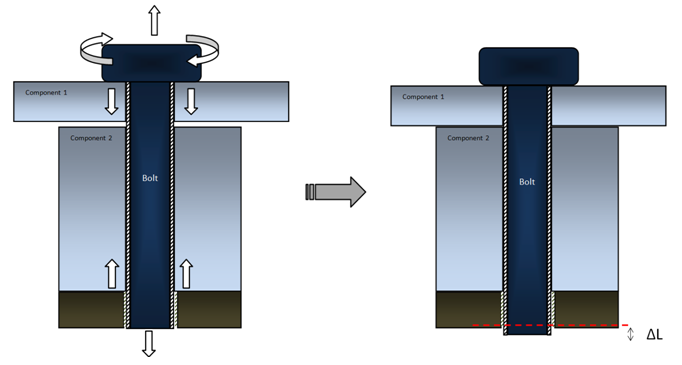
In this case, the shortening (removal of material) of the working part of the bolt happens at the thread within the base, rather than at the bolt-nut interface. Yet the final mechanical effect is the same.
Sometimes the pretensioning by torque/force is augmented by "tightening" via specified number of turns. This means that on top of the , due to pretensioning force, an additional ' is added according to the number of turns and the pitch of the thread.
In an automated assembly process, usually all bolts are pretensioned simultaneously. Sometimes, however, the tensioning may happen in sequence or in groups. In such cases, while is "locked" for bolts that have already been pretensioned, consecutive pretensioning force is applied to the next batch of bolts, which then become "locked" for the following step.
FEA Solution with Pretensioning
In analysis of structures, the FEA model is usually defined in material reference frame and the amount of material is assumed to remain fixed, while the structure undergoes stretching and deformation.
However, in the case of pretensioning, the actual working part of the model has some material removed by being driven through the nut (usually the protruding part of the bolt is not included in the working FEA model, since it does not participate in the balance of forces on the structure).
The simulation of this phenomenon in OptiStruct follows the approach described below:
- 1D Bolt Pretensioning
- 3D Bolt Pretensioning
Multiple point constraints (MPC's) are used in both 1D and 3D pretensioning, the difference between the two implementations is the number of duplicate grid points created and controlled via MPC's.
1D Bolt Pretensioning
The bolt or its selected section is represented by single or multiple 1D element(s) (beam or rod).
Step 1
- First, an imaginary cut is introduced into the beam (This is automatically
done internally for a subcase that includes a PRETENSION
command) and two duplicate grid points are created at the location of the
cut.
Figure 4. FEA Implementation of Bolt Pretensioning Applied to a 1D Bolt using a 1D Element 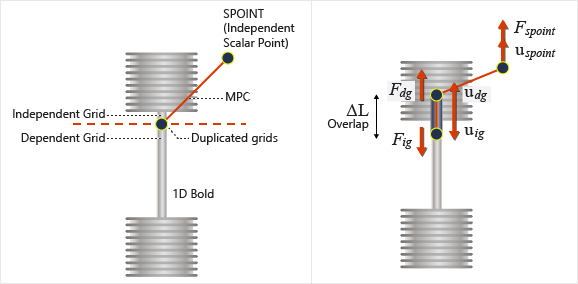
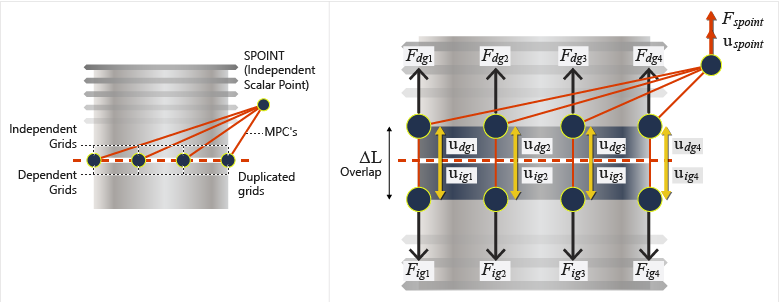
Additionally, a scalar point (SPOINT) is automatically created to act as an independent grid point. A pair of self-balanced pretensioning forces is applied to both ends of the cut with the help of the newly created SPOINT. The specified pretensioning force is internally applied on the SPOINT and this is transferred to the duplicated grid points via an MPC. The MPC controls the movement of the newly created duplicate grid points and the scalar point based on:
Where,- Displacement of the independent scalar point (SPOINT)
- Displacement of the dependent grid point
- Displacement of the independent grid point
The reaction force on the scalar point due to an enforced displacement of on it can be shown to be equal to the forces acting on the dependent or independent grid point.
or depending on the direction of the forces.
Where,- Total reaction force on the independent scalar point (SPOINT) due to an enforced displacement of
- Force acting on the dependent grid point
- Force acting on the independent grid point
- With these forces (plus other loads referenced in this subcase) applied,
static analysis is performed to calculate deformation of the structure.
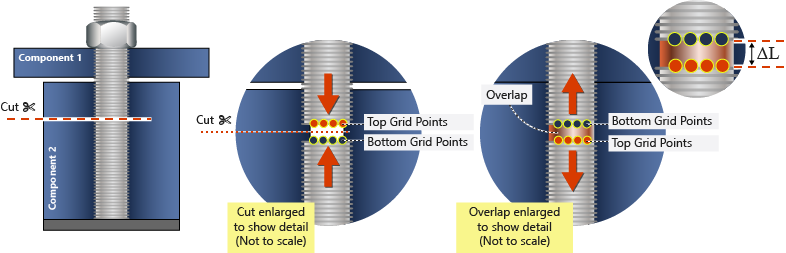
Among the results of such analysis is the "overlap"
across the cut portion of the beam, which is
equivalent to the distance that the bolt would move relative to the nut in
Figure 1.
Figure 5. FEA Implementation of Bolt Pretensioning Applied to a 3D Bolt using a 1D Element (Step 1) 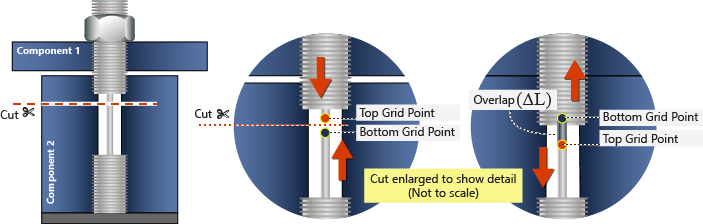
Step 2
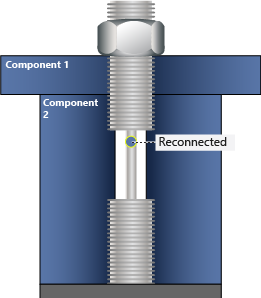
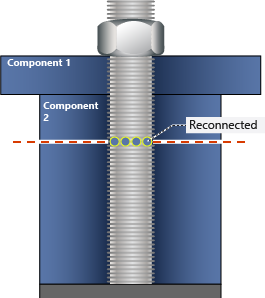
In Figure 5, the amount of overlap calculated in Step 1 is removed from the bolt length, and the bolt is reconnected at the cut location. This represents the shorter working length of a pretensioned bolt on which the nut has been tightened (Mechanically, this is similar to the effect of the DEFORM command).
3D Bolt Pretensioning
In 3D Bolt Pretensioning, the bolt is represented (meshed) using 3D solid elements. A transverse surface in the beam is identified (cross-section) along which it is cut and the duplicate grids are then controlled by Multiple Point Constraints (MPC's) and a SPOINT to simulate the pretensioning effect.
Step 1
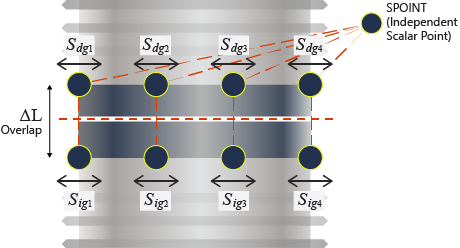
Additionally, a scalar point (SPOINT) is automatically created to act as an independent grid point. A pair of self-balanced pretensioning forces is applied to both ends of the cut with the help of the newly created SPOINT. The specified pretensioning force is internally applied on the SPOINT and this is transferred to the duplicated grid points via MPC's. The MPC's controls the movement of the newly created duplicate grid points and the scalar point based on the following equations.
In the pretension direction:
Perpendicular to the pretension direction:
- Displacement of the independent scalar point (SPOINT)
- Displacement of the th dependent grid point
- Displacement of the th independent grid point
- Displacement of the th independent grid point
- Displacement of the th dependent grid point perpendicular to the pretension direction
- Displacement of the th independent grid point perpendicular to the pretension direction.
The reaction force on the scalar point due to an enforced displacement of on it can be shown to be equal to the sum of the magnitudes of the forces acting on either the dependent or independent grid points.
- Total reaction force on the independent scalar point (SPOINT) due to an enforced displacement of
- Force acting on the th dependent grid point
- Force acting on the th independent grid point
Step 2
As shown in Figure 5, the amount of overlap calculated in Step 1 is removed from the bolt length, and then the bolt is reconnected at the initial cut surface. This represents the shorter working length of a pretensioned bolt on which the nut has been tightened. (Mechanically, this is similar to the effect of the DEFORM command.)
Analysis of Pretensioned Assemblies
The solution of problems involving pretensioning fits into the standard sequences of static subcases, linear or nonlinear. (Step 2, analysis of pretensioned structure, is also available in natural frequency, frequency response, buckling and transient subcases).
Respective user's input requires definition of pretensioning sections, loads and adjustments in the Bulk Data Entry section, plus specification of tensioning sequences in the Subcase Information Entry section. The available commands are outlined below - for more details, see individual card descriptions.
Bulk Data Entry Section
- PRETENS
- Defines the pretension section. Presently this identifies the respective 1D element.
- PTFORCE
- Defines the pretensioning force F (actually a pair of forces) and assigns it to the respective pretension section.
- PTFORC1
- A simplified format that allows assigning force to multiple pretension sections
- PTADJST
- Defines the tensioning adjustment ' and assigns it to the respective pretension section.
- PTADJS1
- A simplified format that allows assigning one adjustment amount to multiple pretension sections.
- PTADD
- Combines multiple pretensioning forces or adjustments into a single load ID.
- PRETPRM, INILOAD
- See the parameter page for more information.
- PRETPRM, PRTSW
- See the parameter page for more information.
Subcase Information Entry Section
- PRETENSION
- Identifies pretensioning forces/adjustments to be activated in this static subcase. (Corresponds to Step 1 described above.)
- STATSUB(PRETENS)
- Identifies the static subcase that created pretensioned bolts, which are to be included in the present subcase. (Corresponds to Step 2 described above.)
It is allowed to have PRETENSION and STATSUB(PRETENS) in the same static subcase - this can be used to emulate more complex pretensioning sequences.
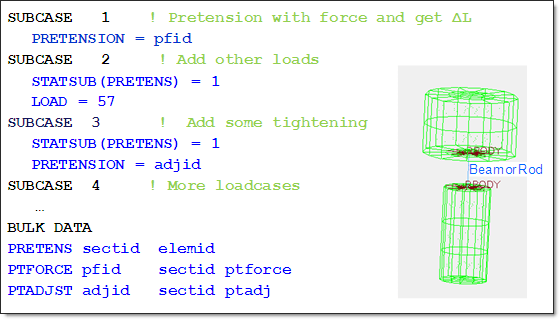
Example: Typical Flow
Comments
Subcases that Support Pretensioning
Pretensioning Steps 1 and 2 require the solution of a static FEA problem. Therefore, PRETENSION and STATSUB(PRETENS) commands can appear only in linear or nonlinear static subcases of the default NLSTAT type.
Reference Pretensioning in Other Subcase Types
Because pretensioning produces stresses in the FEA model, it can through nonlinear geometric stiffness effects, affect the static and vibrational response of the structure, such as increase of natural frequency of a pretensioned bolt. Such geometric stiffness effects are captured by a STATSUB(PRELOAD) command, which is available in static, natural frequencies and frequency response subcases. In problems with pretensioning, it is allowed for STATSUB(PRELOAD) to point to a pretensioned subcase or any of the follow-on static subcases that references pretension. The stresses created by pretension (and other loads in such subcase) will be used as the respective preload.
Pretensioned Subcases Sequences
The subcases with PRETENSION and STATSUB(PRETENS) can be used to create various sequences of pretensioning, such as tightening bolts in sequence or in groups.
A single pretension section (1D bolt) can receive consecutive cumulative pretensioning loads so as to model cases where bolt tightening with a force is followed up by an additional adjustment by a specified distance (number of turns of the nut). Such a stacked sequence is presented in the simple illustration above.
The specific rules for sequencing pretensioning subcases on the same section are:
- If the pretension force (PTFORCE) is applied on some bolts while STATSUB (PRETENS) is defined in the same subcase, those bolts where PTFORCE is applied will have no effect of STATSUB (PRETENS).
- Pretensioning adjustment (PTADJST) may be activated in any of the pretensioning subcases for a given section. The effect of adjustment is cumulative relative to the pretensioning status reached in the respective previous subcase, as referenced by STATSUB(PRETENS).
In nonlinear path-dependent problems, this sequencing of pretensioning can be combined with continuation of nonlinear subcases, as controlled by subcase command CNTNLSUB, in quite arbitrary combination. STATSUB(PRETENS) controls the sequencing of pretensioning steps and CNTNLSUB controls the sequencing of nonlinear aspects (plasticity, contact with friction, and so on) for quite arbitrary loading scenarios.