Cyclic Symmetry Analysis

Cyclic symmetry is a type of symmetry in which a representative (or basic) segment, if patterned circularly about an axis of symmetry would result in the full model.

Structures with symmetry can often be modeled with one representative entity, from which the full structure can be obtained after certain operations (pattern, mirror, rotation, etc.). Such methods can lead to huge savings in modeling effort, computational time, and file storage. Therefore, exploiting symmetry in finite element models could prove to be very advantageous.

Aircraft engine turbines, gas turbine compressor wheels, windmill assembly, vehicle rims, flange joints are some common examples of structures with cyclic symmetry. The images (Figure 1) show the axis of cyclic symmetry and the representative or basic segment.

Figure 1. Cyclic symmetry in a gas turbine compressor wheel

Note:

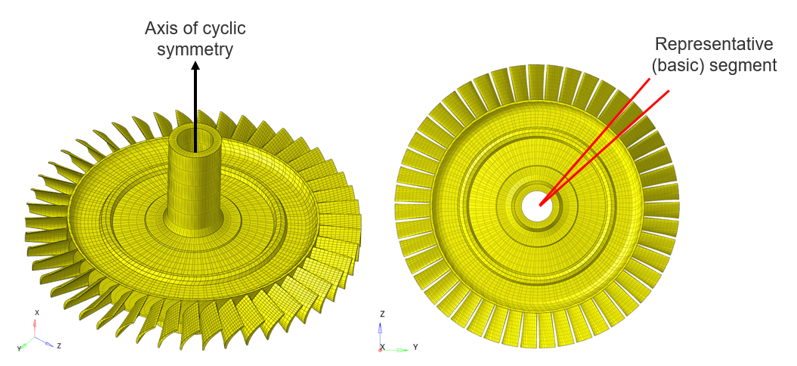
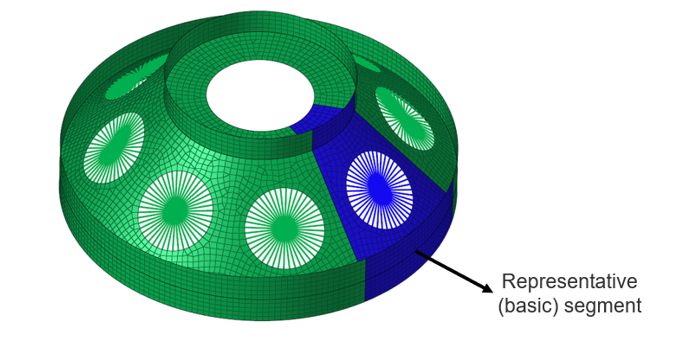
The basic segment could either be the smallest repeating unit in the model or could involve several repeating units.
Depending on your requirements, a full 360 degree model or a partial (as in, 270 degrees) model could be analyzed by suitably specifying the number of segments in the model definition.

In OptiStruct

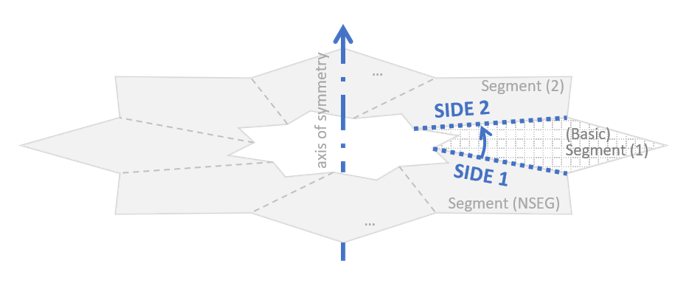
In a cyclic symmetry analysis, the boundaries on either side of the modeled base segment which are to be connected to adjacent segments are defined as SIDE 1 and 2. The direction of the axis of symmetry are determined using the right-hand thumb rule.

If the fingers are curled from SIDE 1 to SIDE 2, then the direction of the thumb determines the direction of the axis of symmetry.

Figure 2. Axis of symmetry and sides of the basic segment

The 1^st segment corresponds to the one which is modeled (base segment). Using the right-hand thumb rule, if the right-hand thumb is along the positive direction of the axis, then the direction of along which the fingers are curled determines the direction along with subsequent segments are numbered (Figure 3).

Figure 3. Numbering of the segments when the axis of symmetry is perpendicular to and out of the plane

In cyclic symmetry analysis, the solution is internally decomposed as a series of harmonic solutions represented using harmonic indices, and they can be requested by the HARMONICS I/O Option.

The harmonic indices are supposed to be non-negative and must be no greater than (NSEG is the number of segments of the actual structure).

If NSEG is odd:

(\frac{N S E G - 1}{2})

If NSEG is even:

(\frac{N S E G}{2})

Further remarks regarding harmonic options for different subcase types are summarized in the table below.


Subcase Type	Non-cyclic Symmetric Behavior	Cyclic Symmetric Behaviour*
Linear Static	Cyclic symmetry analysis can solve for non-cyclic symmetric deformation if non-cyclic symmetric loadings (including non-cyclic symmetric SPCD) exist in the input file. The result is a linear superposition of all the requested harmonic solutions. When all the necessary harmonics are requested, cyclic symmetry linear static analysis is capable of generating deformation identical to a regular linear static analysis which has all the segments of the structure being modelled; therefore, HARMONICS=ALL is usually recommended. In general, harmonics with lower indices contribute more to the result of a linear static cyclic symmetry analysis, and removing some harmonics may lead to loss in accuracy.	If there is no non-cyclic symmetric loading (including non-cyclic symmetric SPCD), all the harmonics vanish except the 0th harmonic, which leads to cyclic symmetric deformation.
Normal Mode	Each harmonic solves for a series of modal shapes of a certain pattern and the result is a collection of modes calculated from the requested harmonic solutions. When all the necessary harmonics are requested, cyclic symmetry normal mode analysis is capable of generating a same number of modes identical to a regular normal mode analysis which has all the segments of the structure being modelled. Removing a certain harmonic index h from the set referenced by HARMONICS would result in the absence in the corresponding mode shapes with h nodal diameters.	The 0th harmonic corresponds to mode shapes with cyclic symmetric mode shapes, that is, no nodal diameter.
Nonlinear Static, Nonlinear Transient	N/A	Only the 0th harmonic (as in, completely cyclic symmetric behaviour) is allowed due to theoretical restrictions.
Preloading/Preloaded Subcase in Prestressed Analyses	Subsequent preloaded subcase can have non-cyclic symmetric deformation or modes.	Preloading must be completely cyclic symmetric due to theoretical restrictions.

*A special case of solving the 0th harmonic only.

The following tables summarize the relevant input file entries in a cyclic symmetry analysis.

Table 1. I/O Options and Subcase Information Entries
Entry	Purpose	Additional Details
HARMONICS	Specifies the solution harmonics to be used.	This entry is optional for cyclic symmetry analysis. By default, all effective harmonics are used.
NOUTPUT	Specifies the segments for which results must be recovered and output.	This entry is mandatory for cyclic symmetry analysis. If a segment is not specified, the results are not recovered and output. Therefore, such segments will not be shown in the result plot.

Table 2. Bulk Data Entries
Entry	Purpose	Additional Details
CYAX	Specifies the grids that lie on the axis of symmetry.	This entry is optional for cyclic symmetry analysis.
CYJOIN	Specifies grid points on the segment boundaries that connect to adjacent segments.	This entry is mandatory for cyclic symmetry analysis. Two entries, one for each side of the segment will be required. Each grid on a CYJOIN entry should be paired with a matching grid on the other entry. The axis of cyclic symmetry is determined by the geometry and `CD` fields of the first pair of grids appearing on CYJOIN entries.
CYSYM	Specifies the number of segments in the model.	This entry is mandatory for cyclic symmetry analysis.
LOADCYH	Specifies the loading by harmonics for linear static analysis.	This entry is used to apply loadings by harmonics in a linear static cyclic symmetry analysis. This can also be used to define gravity and centrifugal loadings. This entry can appear in the same loadset as LOADCYN but cannot share a loadset ID with other type of load entries.
LOADCYN	Defines the loading by segments for linear static analysis.	This entry is used to apply loading by segments in a linear cyclic symmetry analysis. This entry can appear in the same loadset as LOADCYH but cannot share a loadset ID with other type of load entries.
LOAD(ADD)	Defines the loading for implicit nonlinear analyses.	Nonlinear cyclic symmetry subcases do not allow non-cyclic symmetric loadings/behaviors due to theoretical restrictions. Therefore, the regular method of loadset definition is adopted, that is, to directly reference a loadset ID of either load collectors LOAD(ADD)/DLOAD or a set of loads.

Support Information

The current support of cyclic symmetry analysis in OptiStruct is:

Table 3. Support table for cyclic symmetry analysis
Category	Supported Entities	Additional Details
Analysis type	Linear static analysis
	Normal modes analysis	In normal modes analysis, only the Lanczos eigensolver EIGRL and the Lapack-based dense solver EIGRD are supported. Note that field 4, `ND`, on both cards describes the number of roots desired for each harmonic in a cyclic symmetry modal analysis.
	Implicit nonlinear analyses	Nonlinear cyclic symmetric subcases do not support non- cyclic symmetric loadings/behaviors due to theoretical restrictions. Therefore, the regular method of loadset definition is recommended, that is, to directly reference a loadset ID of either load collectors LOAD(ADD)/DLOAD or a set of Bulk Data Entries.
	Prestressed analysis	Either a linear static or implicit nonlinear subcase can be prescribed as a preloading subcase using STATSUB(PRELOAD). The preloading subcase must be completely cyclic symmetric.
Analysis output	DISPLACEMENT STRESS STRAIN Velocity/Acceleration Plasticity related results Contact results	Only .h3d output format is available. Beam element stress/strain is not available. Available in implicit nonlinear analyses for both regular and on-the-fly H3D results.
Elements	CBEAM CTRIA3, CTRIA6 CQUAD4, CQUAD8 CTETRA, CHEXA, CPENTA CPYRA
Constraints	SPC MPC RBE2 RBE3	RBE2 and RBE3 will be generated only for the base segment in the result plot.
Materials	MAT1 MAT2 MAT9 MATT1 MATT2 MATT9
Loads	SPCD Forces Pressures GRAV RFORCE TEMP	GRAV is only supported with rectangular coordinate system. RFORCE is only supported for rotation about the axis of symmetry. Temperature loading must be referenced in the TEMPERATURE(LOAD) Subcase Entry.

Problem Setup

Below is an example of a typical cyclic symmetry analysis setup in an input file.

$ *************************************************************
$ EXAMPLE TO DEMONSTRATE A CYCLIC SYMMETRIC ANALYSIS SETUP
$ *************************************************************
.
.
NOUTPUT     = ALL
SUBCASE      101
  SPC   =  1
  LOAD  = 14

SUBCASE      102
  SPC  =  1
  METHOD(STRUCTURE) = 2
  HARMONICS   = 102

BEGIN BULK
$--1---><---2--><---3--><---4--><--5---><--6---><---7--><--8---><---9-->
CORD2C        11       0     0.0     0.0     0.0     0.0     0.0     1.0
+            1.0     0.0     0.0 

EIGRL          2     0.0              50                             MAX

SET          102    MODE
+              0       1        
CYSYM          4
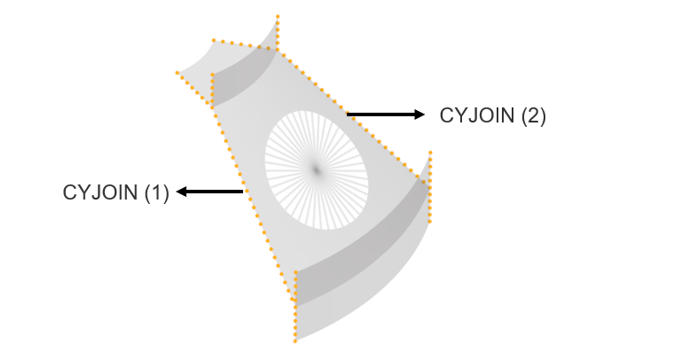
CYJOIN         1              12    THRU      20
CYJOIN         2              22    THRU      30
GRID …
…
 
FORCE         51      12      11     1.0     0.0   100.0     1.0

LOADCYN       14     0.1       2             1.0      51 
LOADCYN       14     0.1       4             1.0      51


.
.

Example

In this example, cyclic symmetric analysis will be demonstrated for the following model which consists of shell elements and RBE2s. The basic segment is chosen to be the smallest repeating unit in the model and is one-eighth of the full model (shown in blue).

The base of the geometry is subjected to fixed supports and a pressure loading is applied on the top face.

Figure 5. Boundary conditions in the model. SPC's shown in red; pressure load is shown in green

The CYJOIN definitions are such that the grid points on each side match with the grid points on the other side. This homologous relationship between the grid points is important and incorrect results could be obtained if this condition is violated.

Figure 6. Grid points in CYJOIN entry on each side of the model

The results from the cyclic symmetry analysis have been compared with a full model as a reference. The results show good agreement.

Figure 7. Comparison of displacements between full model and cyclic symmetric model

Figure 8. Comparison of element stresses between full model and cyclic symmetric model

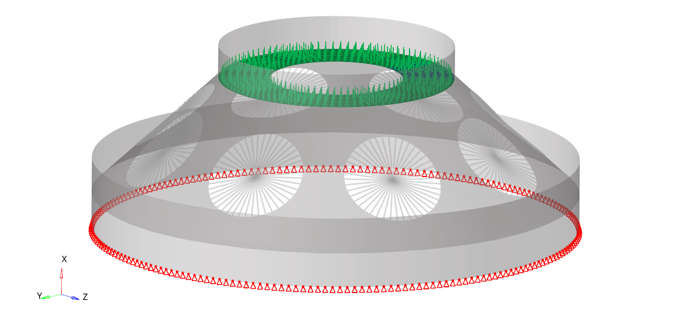
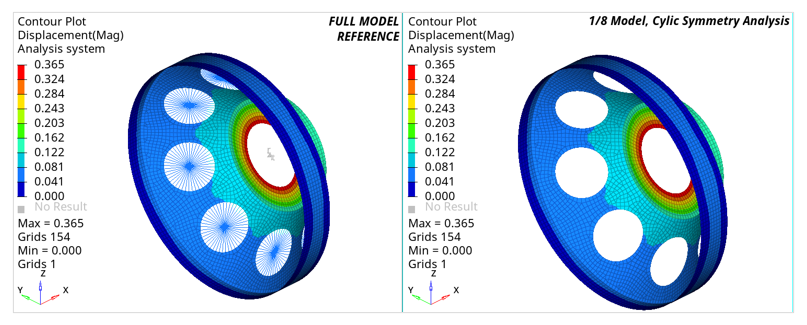
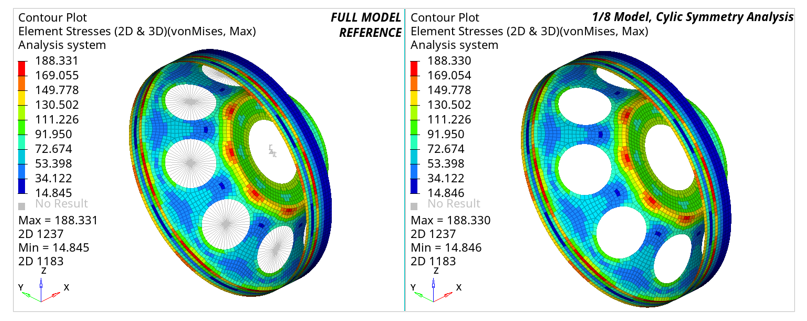
View Results in Cyclic Symmetry Analysis

Systems referenced by the CD field of grid points in the basic segment (including the basic coordinate system when CD is blank) is cyclically patterned and assigned to corresponding grids in each segment requested by NOUTPUT. This can also be used for viewing the results for each segment in its local coordinate system.

To view results in the basic coordinate system, The “Global coordinate system” option can be selected in HyperView.

Comments

HyperMesh support for cyclic symmetry analysis would be available in future releases.