Depuis la version 2026, Flux 3D et Flux PEEC ne sont plus disponibles.
Veuillez utiliser SimLab pour créer un nouveau projet 3D ou pour importer un projet Flux 3D existant.
Veuillez utiliser SimLab pour créer un nouveau projet PEEC (pas possible d'importer un projet Flux PEEC existant).
/!\ La documentation est en cours de mise à jour – des références au 3D peuvent subsister.
Le coefficient de température
Introduction
- leurs correspondants non-dépendant de la température
- complétés par un coefficient de température coeff(T) construit sur la base de deux fonctions exponentielles (description détaillée dans les paragraphes suivants)
Modèle mathématique
- la première, à constante de décroissance négative, est utilisée lorsque coeff(T) varie de 1 à 0.1, c'est-à-dire jusqu'à une température T* égale à TC - 0.10536 C, où C est l'inverse de la constante de décroissance exponentielle du matériau
- la seconde, à constante de décroissance positive, est utilisée au voisinage du point de Curie, lorsque coeff(T) varie de 0.1 à 0, c'est-à-dire au-delà de la température T*
D'un point de vue mathématique, le modèle pour la fonction coeff(T) peut s'écrire comme il suit :
où la température T, la température de Curie TC, ainsi que C (l'inverse de la constante de décroissance exponentielle du matériau) sont exprimées en degrés Celsius °C. Les coefficients
et
sont déterminés afin que les deux exponentielles puissent se raccorder au point où coeff(T*) = 0.1
La constante de décroissance exponentielle de la seconde fonction étant dix fois plus grande que son homologue de la première exponentielle, à la température T* les deux fonctions exponentielles prennent la même valeur, assurant ainsi la continuité du modèle global coeff(T), comme l'illustre la figure ci-dessous.
Paramètres du modèle
- la température de Curie TC du matériau, qui peut être trouvée dans les fiches techniques du fabricant
- et C, qui est l'inverse de la constante de décroissance exponentielle du matériau et qui peut être considérée comme une sorte de constante de température pour décrire à quelle vitesse le matériau perd ses propriétés magnétiques lorsque la température augmente.
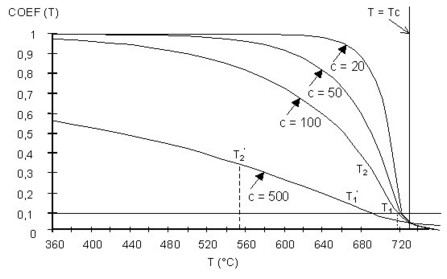
La figure ci-dessous trace la fonction coeff(T) pour TC = 727 °C et plusieurs valeurs pour le paramètre C afin d'illustrer son impact sur les propriétés du matériau dépendant de la température. Plus la valeur de C est faible et plus le matériau conserve ses propriétés magnétiques aux températures proches du point de Curie.