interpn
N dimensional interpolation.
Syntax
Vi = interpn(x1,x2,x3,...,xn,V,x1i,x2i,x3i,...,xin)
Vi = interpn(V,x1i,x2i,x3i,...,xin)
Vi = interpn(V)
Vi = interpn(V,m)
Vi = interpn(...,method)
Vi = interpn(...,method,extrap)
Inputs
- x1,x2,x3,...xn
- The point coordinate values with which to interpolate, with each argument corresponding to a dimension of V.
- V
- The ND grid of function values over which to interpolate.
- x1i,x2i,x3i,...,xni
- The interpolated point coordinates, with each argument corresponding to a dimension of V.
- m
- The number of bisections performed on intervals of V when no coordinate arguments are supplied (default: 1).
- method
- The available options are:
- 'linear' (default)
- Returns the multilinear interpolation.
- 'spline' (not yet available)
- Returns the cubic spline interpolation.
- extrap
- The available options are:
- 'extrapVal' (default: NaN)
- Out of bounds values are set to this scalar value. Setting a value requires use of the method argument.
- 'extrap'
- Allows extrapolation beyond the intervals using the current method.
- 'extrapBound'
- Out of bounds values are confined to the nearest boundary in each dimension.
- 'noextrap'
- Does not allow extrapolation.
Outputs
- Vi
- The interpolated values corresponding to the xni locations.
Examples
Plot interpolated values over a sparsely sampled paraboloid.
x = [-2:0.5:2];
y = [-2:0.5:2];
func = @(x,y) 1 - x.^2 - y.^2;
[xx, yy] = meshgrid(x, y);
V = func(xx,yy);
xi = [-2:0.1:2];
yi = [-2:0.1:2];
Vi = interpn(x, y, V, xi, yi);
[xxi, yyi] = ndgrid(xi, yi);
mesh (xxi, yyi, Vi);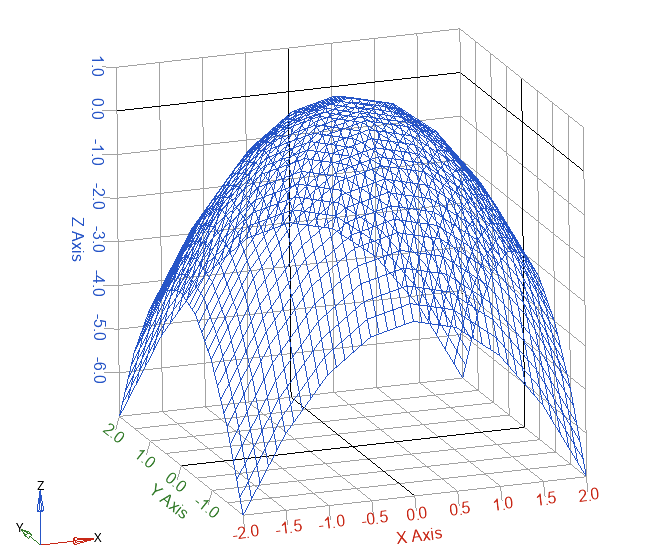
Comments
The function allows interpolation in 1 dimension when V is a column vector, though interp1 would be more efficient.