疲劳材料数据的分散性

处理疲劳测试结果中的分散性。

材料的 SN 和 EN 曲线（以及其他疲劳属性）是从实验（全反转旋转弯曲试验）中获得的。由于试验结果通常伴随着大量分散，因此还应提供数据的统计特征（存活率用于根据曲线的标准误差来估计最差平均对数 (N)，可靠性水平越高，存活率越高）。

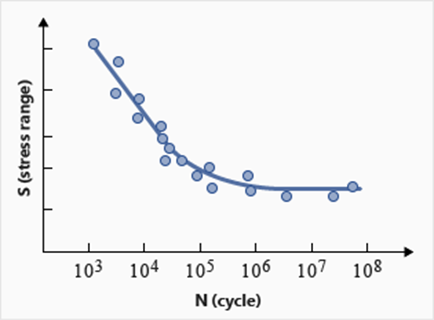
我们以 SN 曲线为例，帮助大家理解这些参数。当 SN 试验数据以交变法向应力振幅 S_a 或范围 S_R 与失效循环数 N 的双对数图表进行表示时，S 和 N 之间的关系可以用直线段进行描述。通常情况下，可以使用一段或两段理想化的线段来描述。

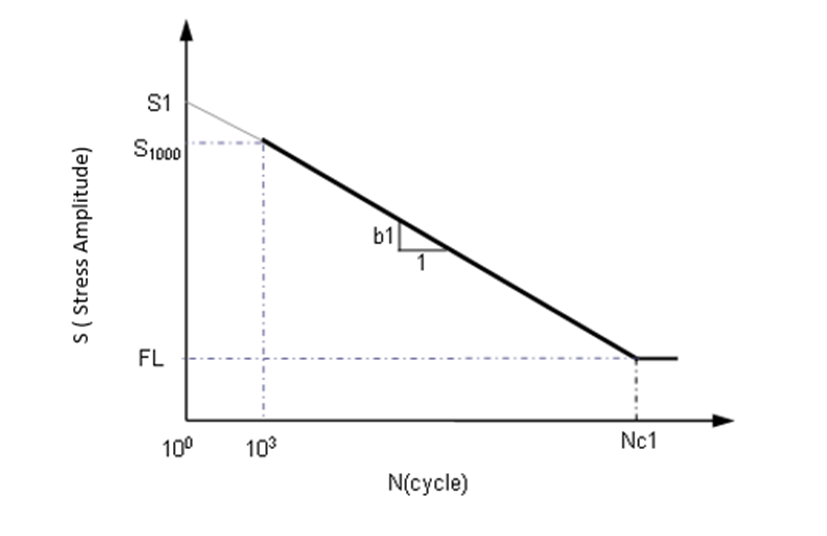
考虑以下情况：SN 的分散性导致同一材料、同一样本的 SN 曲线发生变化。由于自然变化，全反转旋转弯曲试验的结果通常会导致应力振幅 (S) 和寿命 (N) 的数据点发生变化。看看对数尺度，Log(S) 和 Log(N) 中都有变化。具体来说，查看施加了相同应力振幅时寿命的变化，数据点集可能如下所示：


S	Log (S)	Log (N)
2000.0	3.3	3.9
2000.0	3.3	3.7
2000.0	3.3	3.75
2000.0	3.3	3.79
2000.0	3.3	3.87
2000.0	3.3	3.9

与许多流程一样，Log(N) 的分布被假设为正态分布。对于 log(S) 的特定值，log(N) 值可能存在完整总体。完整总体集的均值是真实的总体均值，而且是未知的。因此，可以根据样本的输入样本均值（SN 曲线）和标准误差 (SE)，对 log(N) 的最差真实总体均值进行统计估计。SN 材料数据输入是基于用于生成数据的特定样本中分散的正态分布的均值。

图 3. 特定用户自定义样本数据的 SN 分散性的 Log(N) 正态分布的概率函数

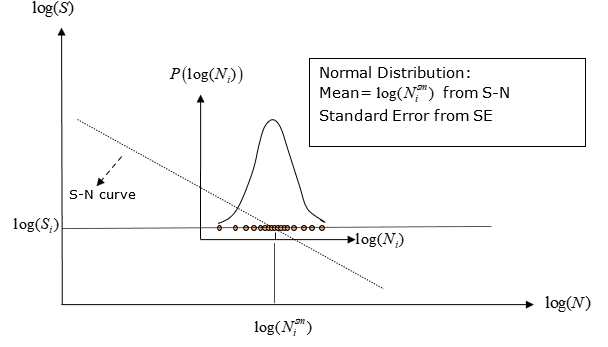
应力振幅和寿命数据中都存在实验散点。需要输入 log(N) 散点的标准误差（SE 字段对应 SN 曲线）。样本均值由 SN 曲线提供，为 $\log (N_{i}^{s m})$ ，而标准误差则通过 SE 字段输入。

如果直接使用指定的 SN 曲线，没有任何扰动，则直接使用样本均值，获得 50% 的存活率。这意味着不会扰乱提供的样本均值。由于 50% 的存活率值可能不足以满足所有的应用，SimSolid可以在内部干扰 SN 材料数据，使其达到您定义的所需的存活率。为此，需要提供以下数据：

log(N) 正态分布标准误差 SE
分析所需的存活率

正态分布或高斯分布是概率密度函数，这意味着曲线下的总面积始终等于 1.0。

定义的 SN 曲线数据被假设为正态分布，其典型特征通常为以下概率密度函数：

P (x_{s}) = \frac{1}{\sqrt{2 π σ_{s}^{2}}} e^{- \frac{{(x_{s} - μ_{s})}^{2}}{2 σ_{s}^{2}}}

其中：

$x_{s}$ 是所定义的样本的数据值（ $\log (N_{i})$ ）。

$μ_{s}$ 是样本均值（ $\log (N_{i}^{s m})$ ）。

$σ_{s}$ 是样本的标准偏差（未知，因为您只输入标准误差[SE]）。

上述分布是您定义的样本的分布，而不是总体空间的分布。由于真实总体均值是未知的，因此要根据样本均值和样本 SE 来估计真实总体均值的范围，然后使用您定义的存活率来扰动样本均值。

标准误差是从总体中抽取的样本的所有均值所形成的正态分布的标准误差。根据单个样本分布数据，标准误差通常被为估算为 $S E = (\frac{σ_{s}}{\sqrt{n_{s}}})$ ，其中 $σ_{s}$ 是样本的标准偏差， $n_{s}$ 是样本中数据值的数量。所有样本均值的这种分布的均值实际上与真实的总体均值相同。提供的存活率适用于所有样本均值的这种分布。

通常，要将一个正态分布函数转换为一个标准正态分布曲线（这是一个平均值 = 0.0，标准误差 = 1.0 的正态分布)。然后可以通过 Z 表直接使用存活率。

注：存活率等于所需的样本目标点之间的概率密度函数下的曲线面积。可以直接计算正态分布曲线的面积（无需转换为标准正态曲线），然而，与标准查找表 Z 表相比，这需要大量的计算。因此，通常要先将当前正态分布转换为标准正态分布，然后使用 Z 表对输入存活率进行参数化。

对于所有样本均值的正态分布，该分布的均值与真实总体均值 $μ$ 相同，要估算的就是它的范围。

在统计学上，可以估计真实总体均值的范围，如下所示：

\log (N_{i}^{s m}) - z * S E \leq μ \leq \log (N_{i}^{s m}) + z * S E

即，

\log (N_{i}^{s m}) - z * S E \leq \log (N_{i}^{m}) \leq \log (N_{i}^{s m}) + z * S E

由于左侧的值比较保守，因此使用以下公式来扰动 SN 曲线：

\log (N_{i}^{m}) = \log (N_{i}^{s m}) - z * S E

其中，

$\log (N_{i}^{m})$ 是被扰乱的值

$\log (N_{i}^{s m})$ 是所定义的样本均值（SN 曲线）

$S E$ 是标准误差 (SE)

z

的值是根据存活率的输入值从标准正态分布 Z 表中获得。下表说明了存活率值相应的一些典型 Z 值。


Z 值（已计算）	存活率（输入）
0.0	50.0
-0.5	69.0
-1.0	84.0
-1.5	93.0
-2.0	97.7
-3.0	99.9

注意 SN 曲线如何被修改为所需的存活率和标准误差输入。通过此方法，您可以使用统计方法处理疲劳材料数据的分散性，预测所需存活率值的数据