应变-寿命 (EN) 方法

应变-寿命分析是基于以下事实：缺口根部等许多关键部位存在应力集中，从而导致在疲劳失效前的循环载荷过程中会产生明显的塑性变形。弹塑性应变结果是进行应变-寿命分析的基础。

Neuber 修正

Neuber 修正是将弹性分析结果修正为弹塑性结果的最普遍的做法。

为了从更容易获得的法向应力推导出局部应力，引入了集中因子，例如局部应力集中因子 $K_{\sigma }$ 和局部应变集中因子 $K_{\epsilon }$ 。

其中， $\sigma$ 指局部应力， $\epsilon$ 指局部应变，S 指法向应力，e 指法向应变。如果法向应力和局部应力都是弹性的，则局部应力集中因子等于局部应变集中因子。但是，如果存在塑性应变，则 $K_{\sigma }$ 和 $K_{\epsilon }$ 之间的关系便不再成立。后来，针对这种情况，Neuber 在理论上引入了弹性应力集中因子$K_t^{}$ 定义如下：

将 Equation 1 和 Equation 2 代入 Equation 3，理论应力集中因子 $K_t^{}$ 可被重写为：

线性静态分析提供的是局部应力而非法向应力，这意味着可以消除 Equation 4 中的几何体的影响，因此可以将 $K_t^{}$ 设置为 1，并将 Equation 4 重写为：

其中， ${\sigma }_e$ ， ${\epsilon }_e$ 是通过弹性分析得到的局部弹性应力和局部弹性应变， $\sigma$ ， $\epsilon$ 是存在塑性应变时的应力和应变。 $\sigma$ 和 $\epsilon$ 都可以根据公式 9 以及循环应力-应变曲线和滞后回线方程进行计算。

循环应力-应变曲线

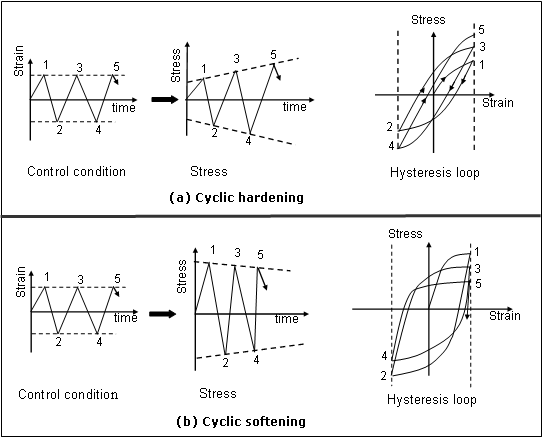
会出现哪种反应取决于材料的性质和热处理的初始条件。下图说明了循环硬化和循环软化的效果，其中绘制了两种不同材料的前两个滞后回线。在这两种情况下，应变被约束在固定范围内变化，而应力可任意变化。在固定应变范围内，如果应力振幅相对于前一个循环增大，如材料循环响应 (a) 所示，则被称为循环硬化；否则，被称为循环软化 (b)。

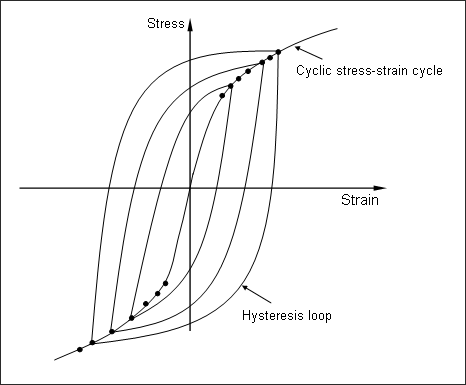
材料的循环响应也可以通过指定应力振幅并保持应变不受约束来描述。在固定应力范围内，如果应变振幅相对于前一个循环增大，则称为循环硬化；否则，称为循环软化。事实上，材料的循环行为会在很短时间内达到稳定状态，这一般占材料总寿命的 10% 以下。通过指定不同的应变振幅，可以得到一系列状态稳定的滞后回线。通过将这些滞后回线放置在一个坐标系中（如 Figure 2所示），连接这些滞后回线的所有顶点的线将决定循环应力-应变曲线。

这可以用类似于单调应力-应变曲线的形式进行表示：

滞后回线形状

Bauschinger 观察到，在初始载荷引起塑性应变后，载荷反转会导致材料表现出各向异性行为。根据实验证据，Massing 提出了一个假设：应力-应变滞后回线在几何上类似于循环应力应变曲线，但幅度是后者的数量两倍。这意味着当数量$\left(\text{Δ}\epsilon ，\text{Δ}\sigma \right)$ 是$\left(\epsilon ，\sigma \right)$ 的两倍时，应力-应变循环将位于滞后回线上。这可以用公式来表达：

$\sigma$ 表达为 $\text{Δ}\sigma$ ， $\epsilon$ 表达为 $\text{Δ}\epsilon$ 并将其代入 Equation 6，滞后回线公式的计算方法为：

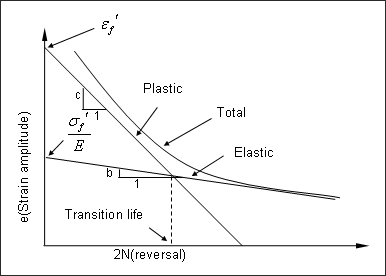
近一个世纪以前，Basquin 观察到，当应力有限时，应力与疲劳寿命在对数尺度上呈线性关系。他提出了以下受应力控制的疲劳公式：

其中， ${\sigma }_a$ 指应力振幅， $\sigma {\text{'}}_f$ 指疲劳强度系数，b 指疲劳强度指数。在 20 世纪 50 年代，Coffin 和 Manson 分别提出，塑性应变也可能与疲劳寿命呈简单的幂律关系：

其中， ${\epsilon }_a^p$ 指塑性应变振幅，$\epsilon {\text{'}}_f$ 指疲劳延性系数， 指疲劳延性指数。Morrow 结合了 Basquin、Coffin和 Manson 的工作，综合考虑了弹性应变和塑性应变对疲劳寿命的作用。他发现总应变与疲劳寿命有更直接的关系。可以使用胡克定律将 Basquin 规则改写为：

其中， ${\epsilon }_a^e$ 指弹性应变振幅。总应变幅度是弹性应变和塑性染色的总和，因此可以使用 Basquin 公式和 Coffin-Manson 公式来描述：

其中， ${\epsilon }_a$ 是总应变振幅，其他变量与上述相同。