随机响应疲劳分析

随机响应分析的功率谱密度 (PSD) 结果用于计算力矩 $m_{n}$ 这些力矩用于生成周期数与应力范围的概率密度函数。

根据随机响应分析中产生的 PSD 应力计算 PSD 力矩。

功率谱密度 (PSD) 力矩

根据随机响应分析中产生的应力 PSD 计算 PSD 力矩为：

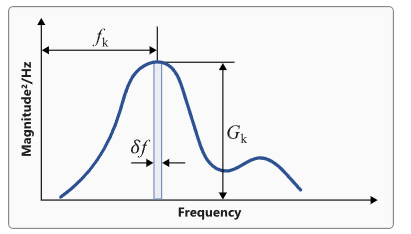
力矩的计算依据为：(1)

m_{n} = \sum_{k = 1}^{N} f_{k}^{n} G_{k} δ f

其中，

$f_{k}^{}$: 频率值。
$G_{k}$: 特定频率下的 PSD 响应值 $f_{k}^{}$ 。

计算应力范围出现概率

针对每个循环段内初始和最终应力范围值之间的应力范围出现概率的计算是用户定义的。

P (Δ S_{i})

在

(Δ S_{i} - δ S / 2)

和

(Δ S_{i} + δ S / 2)

之间的应力范围出现的概率为： (2)

P (Δ S_{i}) = p δ S_{i}

概率密度函数（周期数与应力范围的概率密度）

以如上方式计算的 PSD 力矩用于应力范围概率密度函数 $f (m_{n})$ 的生成。此函数基于指定的损伤模型。DIRLIK、LALANNE、NARROW 和 Steinberg 三波段 (THREE) 选项用于定义损伤模型。

DIRLIK

DIRLIK 提出了用于确定概率密度函数的封闭形式的解，即：(3)

p (S) = \frac{\frac{D_{1}}{Q} e^{\frac{- Z}{Q}} + \frac{D_{2} Z}{R_{2}} e^{\frac{- Z^{2}}{2 R^{2}}} + D_{3} Z e \frac{- Z^{2}}{2}}{2 \sqrt{m_{0}}}

其中，

$D_{1} = \frac{2 (x_{m} - γ^{2})}{1 + γ^{2}}$
$D_{2} = \frac{1 - γ - D_{1} + D_{1}^{2}}{1 - R}$
$D_{3} = 1 - D_{1} - D_{2}$
$Z = \frac{S}{2 \sqrt{m_{0}}}$
$Q = \frac{1.25 (γ - D_{3} - D_{2} R)}{D_{1}}$
$R = \frac{γ - x_{m} - D_{1}^{2}}{1 - γ - D_{1} + D_{1}^{2}}$
$x_{m} = \frac{m_{1}}{m_{0}} \sqrt{\frac{m_{2}}{m_{4}}}$
$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$: 不规则因子。
$S$: 应力范围。

LALANNE

LALANNE 随机疲劳损伤模型将概率密度函数描述为：(4)

p (S) = \frac{1}{\sqrt{m_{0}}} \frac{\sqrt{1 - γ^{2}}}{\sqrt{2 π}} e^{\frac{- S^{2}}{8 m_{0} (1 - γ^{2})}} + \frac{S_{γ}}{4 \sqrt{m_{0}}} (1 + e r f (\frac{S γ}{2 \sqrt{2 m_{0} (1 - γ^{2})}}))

其中，

$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$: 不规则因子。
$S$: 应力范围。

NARROW

窄带随机疲劳损伤模型使用以下概率函数：(5)

p (S) = (\frac{S}{4 m_{0}} e^{- (\frac{S^{2}}{8 m_{0}})})

其中，

$S$: 应力范围。

默认情况下，对于窄带 (NARROW)，使用零交叉数

n_{z c r o s s} = \sqrt{m_{2} / m_{0}}

而非峰值数

n_{p e a k s} = \sqrt{m_{4} / m_{2}}

，因为涉及的数字计算

m_{4}

有时可能会导致不稳定的数值行为。如果信号是理想的窄带，零交叉数和峰值数应该几乎相等。

THREE

Steinberg 三波段随机疲劳损伤模型使用以下概率函数：(6)

P (S) = \{\begin{matrix} 0.683 a t 2 \sqrt{m_{0}} \\ 0.271 a t 4 \sqrt{m_{0}} \\ 0.043 a t 6 \sqrt{m_{0}} \end{matrix}

其中，

$S$: 应力范围。

和其他损伤模型不同，对于三波段 (THREE)，这些值为概率（而非概率密度）。在其他损伤模型中使用大写字母

P (S)

相较于小写字母

p (S)

也很明显。

对于三频带 (THREE) 损伤模型，这些概率直接用于计算周期数，

P (S)

与整个时间关系中的零交叉数相乘。对于其他损伤模型（除 THREE 之外），概率密度值首先乘以

D S

（循环大小）以计算概率。

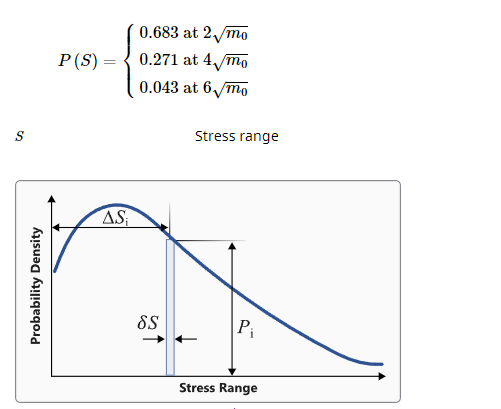
概率密度函数可以根据随机响应疲劳求解设置中定义的以下参数进行调整。

上曲面应力范围因子

应力范围上限的计算方式为：

应力范围上限 = 2*RMS 应力*上曲面应力范围因子

RMS 应力是由随机响应子工况输出的。目标应力范围受限于应力范围的上限。在疲劳损伤计算中，将不考虑任何超出上限的应力。

上曲面应力范围

直接指定上曲面应力范围。

循环次数

计算要计算相应概率的应力范围宽度 $D S = δ S$ （参见 Figure 2）。默认值为 100，第一个循环从 0.0 开始，至 $δ S$ 。应力范围宽度计算为：DS=上曲面应力范围/循环次数

应力范围宽度

直接定义应力范围的宽度 ( $δ S$ )。

计算应力范围出现概率

针对每个循环段内初始和最终应力范围值之间的应力范围出现概率的计算是基于损伤模型的。

DIRLIK, LALANNE, NARROW: $P (S_{i})$ 在 $(Δ S_{i} - δ S / 2)$ 和 $(Δ S_{i} + δ S / 2)$ 之间的应力范围出现的概率为： (7)
$P (S_{i}) = p_{i} (S_{i}) δ S$
THREE: 参阅 Equation 6。; 对于 THREE 损伤模型，仅有三个循环。每个应力范围（2*RMS、4*RMS 和 6*RMS）的周期数是通过直接将相应的概率与总的零交叉数相乘来计算的（有关零交叉数的计算，请参阅下面的部分）。

选择损伤模型

以下信息可能帮助选择损伤模型。

应力的 PSD 力矩用于计算相应的力矩，这些力矩用于确定应力范围的概率密度函数。
DIRLIK 和 LALANNE 模型在更广泛的应力范围谱系分布中产生概率。因此，当输入的随机信号由多个频率的各种应力范围组成时，应使用这些模型。如果使用 DIRLIK 和 LALANNE，概率密度函数中的信息能更好地捕捉到应力范围分布的更广范围。
NARROW 模型适用于应力范围预计与特定应力范围分布的高概率密切相关的随机信号。因此，如果您知道输入的随机数据没有广泛的应力范围分布，而是主要集中在某个特定的应力范围，则应该选择 NARROW。这个模型预计最高的应力范围概率位于这个特定的应力范围或其周围。
THREE 模型与 NARROW 模型相同，只是它预计随机信号的分布除了包含与 1*RMS 的关联外，还包含与 2*RMS 和 3*RMS 的关联（尽管关联较小）。因此，如果您的输入随机数据主要集中在 1*RMS 的应力范围内，其次是 2*RMS 和 3*RMS，那么您应该选择 THREE。

峰值数和零交叉数

NARROW, THREE

原始时域随机载荷（基于频率的随机 PSD 载荷由其产生）中的每秒零交叉数确定为：(8)

n_{z c r o s s} = \sqrt{\frac{m_{2}}{m_{0}}}

其中，

$m_{n}$: 计算出的相应力矩。

DIRLIK, LALANNE

原始时域随机载荷（基于频率的随机 PSD 载荷由其产生）中的每秒峰值数确定为：(9)

n_{p e a k s} = \sqrt{\frac{m_{4}}{m_{2}}}

其中，

$m_{n}$: 计算出的相应力矩。

周期数

窄带 (NARROW)，三波段 (THREE)

总周期数计算为：(10)

N_{T} = n_{z c r o s s} T

其中，

T: 总曝光时间。

DIRLIK, LALANNE

总周期数计算为：(11)

N_{T} = n_{p e a k s} T

其中，

T: 总曝光时间。

特定应力范围的总周期数

应力范围

Δ S_{i}

的总周期数计算为：(12)

N_{i} = P (Δ S_{i}) N_{T}

疲劳寿命和损伤

疲劳寿命（材料在失效前的特定应力范围

S_{i}

的最大周期数）根据材料 SN 曲线计算为：(13)

N_{f} (S_{i}) = {(\frac{S_{i}}{S_{f}})}^{\frac{1}{b}}

作为施加的随机载荷的结果，总疲劳损伤计算为： (14)

D = \sum_{i = 1}^{N} \frac{N_{i}}{N_{f} (S_{i})}

为了将任何导致平均应力不为零的载荷的平均应力修正考虑在内，您可以定义一个由这种载荷（通常是重力载荷）组成的静态子工况。这个静态子工况可以在随机疲劳分析事件设置中引用。