平均应力修正

可使用平均应力修正来说明非零平均应力的影响。

一般情况下，可通过完全反转的循环载荷的标准试验得到疲劳曲线。然而，真实的疲劳载荷不能完全反转，法向平均应力对部件的疲劳性能有显著影响。就疲劳强度而言，拉伸法向平均应力是有害的，而压缩法向平均应力是有益的。可使用平均应力修正来说明非零平均应力的影响。

根据材料、应力状态、环境和应变振幅的不同，疲劳寿命通常取决于沿剪切面或拉伸面出现的微裂纹生长。临界平面平均应力修正方法结合了支配这两类裂纹生长的主要参数。由于可能的失效模式不同（以剪切或拉伸为主），不能指望使用单一的平均应力修正方法来关联所有材料在所有生命周期中的试验数据。关于多轴疲劳寿命估算的最佳方法，目前还没有达成共识。对于基于应力的平均应力修正方法，拉伸裂纹可使用 Goodman 和 FKM 模型。剪切裂纹可使用 Findley 模型。对于基于应变的平均应力修正法，拉伸裂纹可使用 Morrow 模型和 Smith-Watson-Topper 模型。剪切裂纹可使用 Brown-Miller 模型和 Fatemi-Socie 模型。如果定义了多个模型，SimSolid 会从所有可用的损害值中选择造成最大损害的模型。

Goodman 模型

可使用 Goodman 模型评估临界平面上拉伸裂纹生长造成的损害。

S_{e} = \frac{S_{a}}{(1 - \frac{S_{m}}{S_{U}})} ↵

其中：

$S_{m}$ 是平均应力，公式为 $S_{m} = (S_{m a x} + S_{m i n}) / 2$
$S_{a}$ 是应力振幅
$S_{e}$ 是平均应力校正后的应力振幅
$S_{u}$ 是极限振幅

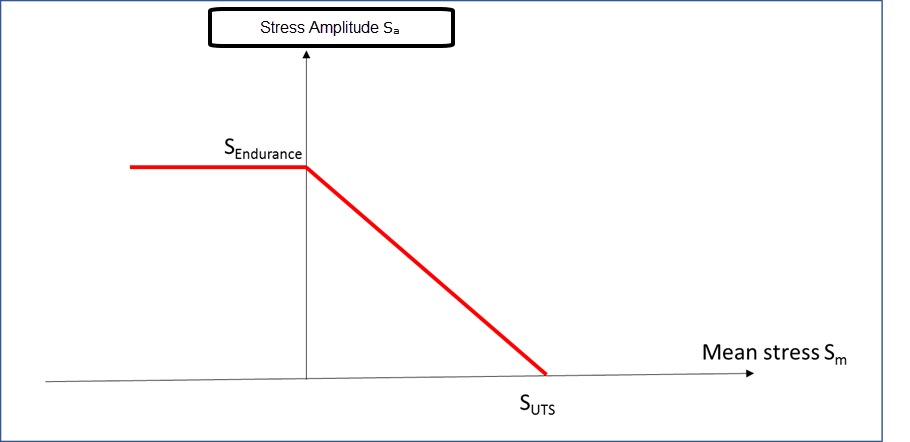
Goodman 模型总是以加速疲劳失效的方式来处理正平均应力修正，而忽略负平均应力。这种方法提供了压缩平均应力的保守结果。

Haigh 图表描述了在给定的失效循环次数下，应力振幅和平均应力的不同组合。

Findley 模型

Findley 准则通常适用于有限寿命疲劳的情况。每个平面的方程如下：

\frac{Δ τ}{2} + k σ_{n} = τ_{f}^{*} {(N_{f})}^{b}

其中：

τ_{f}^{*}

是由剪切疲劳强度系数

τ_{f}^{'}

计算得出，使用：

τ_{f}^{*} = \sqrt{1 + k^{2}} τ_{f}^{'}

修正因子

\sqrt{1 + k^{2}}

通常的设定值约为 1.04。

注：

τ_{f}^{*}

必须根据振幅来定义。如果

τ_{f}^{'}

不是由用户来定义，则 SimSolid 使用以下公式进行计算：

(30)

\begin{array}{l} τ_{f}^{'} = C f * 0.5 * S R I 1 \\ 其中, \\ C f = \frac{2}{1 + \frac{k}{\sqrt{1 + k^{2}}}} \end{array}

常数 k 由实验得出，即执行涉及两种或两种以上应力状态的疲劳试验。对于延性材料，k 通常在 0.2 和 0.3 之间变化。

FKM

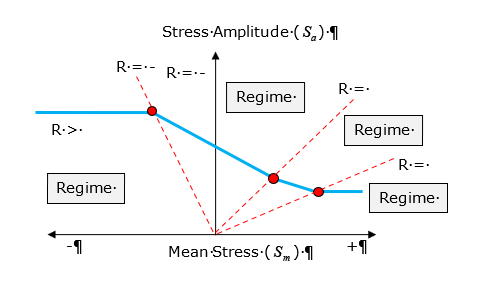
据 FKM 准则，根据应力比 (R=SMIN/Smax) 值将 Haigh 图表分为四个区域。然后使用修正后的值选择损害和寿命计算阶段的 SN 曲线。

下面的 FKM 方程说明了修正应力振幅的计算过程 ( $S_{e}^{A}$ )。损害计算中使用的实际应力值是修正的应力振幅（即 $2 \cdot S_{e}^{A}$ )。这些公式适用于所输入的 SN 曲线。

区域 1 (R>1.0)： $S_{e}^{A} = S_{a} (1 - M)$

区域 2 (-∞≤R≤0.0)： $S_{e}^{A} = S_{a} + M * S_{m}$

区域 3 (0.0<R<0.5)： $S_{e}^{A} = (1 + M) \frac{S_{a} + (\frac{M}{3}) S_{m}}{1 + \frac{M}{3}}$

区域 4 (R≥0.5)： $S_{e}^{A} = \frac{3 S_{a} {(1 + M)}^{2}}{3 + M}$

其中

S_{e}^{A}

是平均应力校正后的应力振幅（耐久应力），

S_{m}

是平均应力，

S_{a}

是应力振幅，M 是平均应力敏感度。

Morrow

Morrow 率先通过在疲劳强度系数中引入平均应力 $σ_{0}$ 来考虑平均应力的影响，公式为：

ε_{a}^{e} = \frac{(σ'_{f} - σ_{0})}{E} {(2 N_{f})}^{b}

因此，整个疲劳寿命公式变为：

ε_{a} = \frac{(σ_{f}^{'} - σ_{0})}{E} {(2 N_{f})}^{b} + ε_{f}^{'} {(2 N_{f})}^{c}

Morrow 方程与观察结果一致，即平均应力效应在塑性应变处于低值时影响显著，在塑性应变处于高值时影响很小。

MORROW2 ：改进了 Morrow 方法，忽略了负平均应力的影响。

Smith、Watson 和 Topper

Smith、Watson 和 Topper 提出了一种不同的方法，通过考虑一个周期内的最大应力来解释平均应力的影响（方便起见，以下将该方法简称为 SWT）。在这种情况下，损害参数被修改为最大应力和应变振幅的乘积。

ε_{a}^{S W T} σ_{\max} = ε_{a} σ_{a} = σ_{a} (\frac{σ'_{f}}{E} {(2 N_{f})}^{b} + ε'_{f} {(2 N_{f})}^{c})

SWT 方法预测当最大应力为零或负值时不会发生损害，这与实际情况不符。

当比较这两种方法时，SWT 方法预测了以拉伸为主的载荷的保守寿命，而当载荷以压缩为主时，Morrow 方法提供了更现实的结果。

Fatemi-Socie

该模型适用于剪切裂纹生长。在剪切载荷过程中，形状不规则的裂纹表面会产生摩擦力，这样会减少裂纹尖端的应力，从而阻碍裂纹生长，增加疲劳寿命。拉伸应力和应变会使裂纹表面分开，减少摩擦力。目前已经获得了这种行为的断口分析证据。对于因纯扭力而失效的物体，可以在断口看到大范围的摩擦，与在断口表面观察到单个滑移带的拉伸试验断口相比，前者相对平淡无奇。

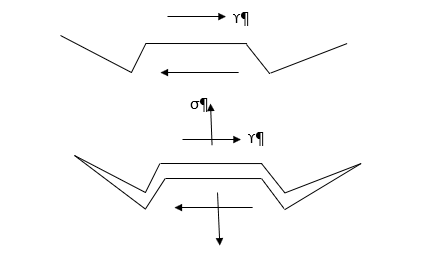
为了验证最大应力的影响，进行了六次拉伸-扭力载荷历史的试验。它们被设计成具有相同的最大剪切应变振幅。在六个载荷历史中，循环法向应变也是恒定的。实验得到的最大剪切应变振幅、等效应力和应变振幅以及塑性功基本一致。载荷历史的主要区别在于最大剪切应变平面上的法向应力。

载荷历史和法向应力显示在每条裂纹生长曲线顶部的图中。最大应力越高，生长速度越快，疲劳寿命越低。当裂纹萌生为 10 mm 量级（材料中较小的晶粒尺寸）时，最大应力对裂纹萌生的影响较小。

这些观察结果导致了以下模型的出现，该模型可以解释为由法向应力修正的循环剪切应变，目的是为了包括裂纹闭合效应。

\frac{Δ γ}{2} (1 + k \frac{σ_{n, \max}}{σ_{y}}) = \frac{τ_{f}^{'}}{G} {(2 N_{f})}^{b_{γ}} + γ_{f}^{'} {(2 N_{f})}^{c_{γ}}

材料对法向应力的敏感度反映在数值 $k / σ y$ 上。其中， $σ y$ 是 SimSolid 中使用的总应变为 0.002 时的应力。如果无法获得来自多个应力状态的测试数据，则 k=0.3。该模型不仅解释了拉伸载荷和扭力载荷的区别，而且可以用来描述平均应力和非比例硬化效应。只包括应变项的临界平面模型不能反映依赖于硬化的平均应力或应变路径的影响。

选择过渡疲劳寿命 2N_t 是因为弹性应变和塑性应变对疲劳损伤的作用相当。可以从单轴疲劳常数中获得。

2 N_{f} = {(\frac{E ε_{f}^{'}}{σ_{f}^{'}})}^{(\frac{1}{b - c})}

采用 Fatemi-Socie 模型来确定剪切应变常数。

\frac{Δ γ}{2} (1 + k \frac{σ_{n, \max}}{σ_{y}}) = \frac{τ_{f}^{'}}{G} {(2 N_{f})}^{b_{γ}} + γ_{f}^{'} {(2 N_{f})}^{c_{γ}}

首先，注意剪切和拉伸的指数应该是相同的。

\begin{array}{l} b_{γ} = b \\ c_{γ} = c \end{array}

剪切模量直接由拉伸模量计算得出。

G = \frac{E}{2 (1 + ν)}

可以通过单轴循环应力-应变曲线预估屈服强度。

σ_{y} = K^{'} {(0.002)}^{n^{'}} = \frac{σ_{f}^{'}}{ε_{f}^{' \frac{b}{c}}} {(0.002)}^{\frac{b}{c}}

可以根据过渡疲劳寿命和单轴属性计算法向应力和应变。

\frac{Δ ε_{p}}{2} = ε_{f}^{'} {(2 N_{t})}^{c}

\frac{Δ ε_{e}}{2} = \frac{σ_{f}^{'}}{E} {(2 N_{t})}^{b}

σ_{n, \max} = \frac{Δ σ}{4} = \frac{E Δ ε_{e}}{4}

代入适当的弹性和塑性泊松比的值，可得出：

\begin{array}{l} \frac{Δ γ_{e}}{2} = 1.3 \frac{Δ ε_{e}}{2} \\ \frac{Δ γ_{p}}{2} = 1.5 \frac{Δ ε_{p}}{2} \end{array}

将总应变的弹性部分和塑性部分分离，得到剪切应变寿命常数表达式：

\begin{array}{l} τ_{f}^{'} = \frac{1.3 Δ ε_{e}}{2} (1 + k \frac{σ_{n, \max}}{σ_{y}}) \frac{G}{{(2 N_{t})}^{b_{γ}}} \\ γ_{f}^{'} = \frac{1.5 Δ ε_{p}}{2} (1 + k \frac{σ_{n, \max}}{σ_{y}}) \frac{G}{{(2 N_{t})}^{c_{γ}}} \end{array}

Brown-Miller

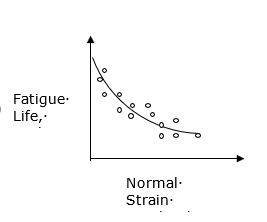
该模型适用于剪切裂纹生长。Brown 和 Miller 在恒定剪切应变范围内进行了拉伸和扭力联合试验。最大剪切应变平面上的法向应变范围会随着施加的拉伸比和扭力比而变化。基于下面显示的恒定剪切应变振幅的数据，Brown 和 Miller 得出结论，由于剪切应变和法向应变会联合降低疲劳寿命，因此需要两个应变参数来描述疲劳过程。

法向应变振幅的影响

与 Findley 针对高周疲劳提出的剪切应力和法向应力类似，他们提出，必须同时考虑最大剪切平面上的循环剪切应变和法向应变。循环剪切应变有助于裂纹成核，而法向应变有助于裂纹生长。他们针对这一理论提出了一个简单的公式：

\frac{Δ \hat{γ}}{2} = \frac{Δ γ_{\max}}{2} + S Δ ε_{n}

其中 $Δ \hat{γ}$

为等效剪切应变范围，S 为材料相关参数，表示法向应变对材料微裂纹生长的影响，通过关联轴向和扭力数据来确定。在这里，

Δ γ_{\max}

被视为最大剪切应变范围，

Δ ε_{n}

是出现了剪切应变范围

Δ γ_{\max}

的平面上的法向应变范围。取适当的泊松比分别考虑弹性应变和塑性应变，结果如下：

\frac{Δ γ_{\max}}{2} + S Δ ε_{n} = A \frac{σ_{f}^{'}}{E} {(2 N_{f})}^{b} + B ε_{f}^{'} {(2 N_{f})}^{c}

其中：

A = 1.3+0.7S

B = 1.5+0.5S

计算平均应力效应时采用了 Morrow 的平均应力方法，即从疲劳强度系数中减去平均应力。最大剪切应变振幅平面上的平均应力， $σ_{n}$ ，为轴向平均应力的一半，得出的公式为：

\frac{Δ γ_{\max}}{2} + S Δ ε_{n} = A \frac{σ_{f}^{'} - 2 σ_{n, m e a n}}{E} {(2 N_{f})}^{b} + B ε_{f}^{'} {(2 N_{f})}^{c}