动力学

可以使用 SimSolid 动力学分析实时评估设计。

设置

指定分析所关联的模态结果。模态解必须存在于当前设计研究中。在 SimSolid 中，运动方程的时间积分极快，且所有模态都包含在分析中。
为频率响应和随机响应指定频率跨度的上限和下限。对于瞬态响应，请指定 Time span。
对于响应谱分析，请指定模态组合类型。如果选择 CQC 方式，则需要设置阻尼比。
使用 Rayleigh 阻尼系数或模态阻尼来指定阻尼。
选中 Evaluate peak responses during solving 复选框，以评估求解阶段的峰值响应。

更多信息请参阅创建分析。

阻尼

支持两种指定阻尼的方法。

Rayleigh 阻尼系数: 假设阻尼矩阵与质量矩阵和刚度矩阵成正比。要使用此方法，需要在动力学创建对话框中指定质量 (F1) 和刚度 (F2) 的值。
模态阻尼: 为每种模式创建临界阻尼比。可以在动力学分析创建对话框中指定该值。

动力学分析注意事项

当基本激励类型为位移时，位移和速度的初始条件始终假设为零。
在 SimSolid 中，边界兼容性近似满足。约束端的响应不会绝对为零，但与峰值响应相比相对较小。
等效辐射功率密度的计算方法为：
$ERP Density = ERPRLF * (0 .5 * ERPC * ERPRHO) * v^{2}$
其中，

$v$

拾取点的法向速度

ERPC（声音在空气中的速度）

343 m/s

ERPRHO（空气密度）

1.225 Kg/m3

ERPRLF（辐射损失系数）

1

计算等效辐射功率就是计算拾取面上的 ERP 密度的积分，如图所示：
$ERP = ERPRLF * (0 .5 * ERPC * ERPRHO) \int_{S} v^{2} d s$
绝对位移的相位可以使用频率动力学的拾取信息进行查询。
频率动力学中的相对位移和绝对位移之间的关系如下。
相对运动计算为：
$\ddot{x} + 2 ζ ω_{n} \dot{x} + ω_{n}^{2} = - \ddot{b}$
其中基础激励 $b$ 为：
$- \ddot{b} = Y_{0} (ω) e^{i (ω t + ϕ)}$
求解这个微分方程，相对位移可以计算为：
$x_{r} (t) = Y_{0} (ω) e^{i ϕ} (\frac{ω_{n}^{2} - ω^{2}}{{(ω_{n}^{2} - ω^{2})}^{2} + {(2 ζ ω_{n} ω)}^{2}} - i \frac{2 ζ ω_{n} ω}{{(ω_{n}^{2} - ω^{2})}^{2} + {(2 ζ ω_{n} ω)}^{2}}) e^{i ω t}$

注：通过将相对运动与基础激励相加来计算绝对运动。
在频率动力学和随机动力学中，复变函数法用于求解微分方程。位移、速度和加速度结果具有复数分量。
已知位移的复数值为：
$D_{x} = a_{x} + i b_{x}$
$D_{y} = a_{y} + i b_{y}$
$D_{z} = a_{z} + i b_{z}$
评估等级和相位 $D_{x}$ 计算公式如下：
$M a g (D_{x}) = |D_{x}| = \sqrt{{a_{x}}^{2} + {b_{x}}^{2}}$
$P h a (D_{x}) = θ_{x} = \tan^{- 1} \frac{b_{x}}{a_{x}}$
以此类推 $D_{y}$ 和右端的 $D_{z}$ 。在 SimSolid 中， $|D_{x}|$ 和右端的 $θ_{x}$ 被导出。
您可以评估 $a_{x}$ 和右端的 $b_{x}$ ，使用以下公式计算：
$a_{x} = |D_{x}| \cos θ_{x}$
$b_{x} = |D_{x}| \sin θ_{x}$
位移大小的计算为：
$|\sqrt{D_{x}^{2} + D_{x}^{2} + D_{x}^{2}}| = \sqrt{|D_{x}^{2} + D_{x}^{2} + D_{x}^{2}|}$
计算公式如下：
${D_{x}}^{2} + {D_{y}}^{2} + {D_{z}}^{2} = {a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2} + i 2 (a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z})$
您获得
$|{D_{x}}^{2} + {D_{y}}^{2} + {D_{z}}^{2}| = \sqrt{{({a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2})}^{2} + {(2 (a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}))}^{2}} = \sqrt{{({a_{x}}^{2} - {b_{x}}^{2} + {a_{y}}^{2} - {b_{y}}^{2} + {a_{z}}^{2} - {b_{z}}^{2})}^{2} + A}$
其中，
$A = - 4 ({a_{x}}^{2} {b_{y}}^{2} + {a_{y}}^{2} {b_{x}}^{2} + {a_{x}}^{2} {b_{z}}^{2} + {a_{z}}^{2} {b_{x}}^{2} + {a_{y}}^{2} {b_{z}}^{2} + {a_{z}}^{2} {b_{y}}^{2} - 2 a_{x} b_{x} a_{y} b_{y} - 2 a_{x} b_{x} a_{z} b_{z} - 2 a_{y} b_{y} a_{z} b_{z})$
示例：
$D_{x} = 1 + 2 i, D_{y} = 3 + 4 i, D_{z} = 1.5 + 3.5 i$
位移大小：44.5
当瞬态动力学分析与预应力模态分析相关联时，会提供一种新结果类型，成为总位移。总位移是预应力位移和动态位移的组合。因此，位移大小是由动态分析引起的位移。
对于随机响应分析，响应的功率谱密度 (PSD) $S_{x o} (f)$ ，与源的功率谱密度有关， $S_{a} (f)$ ，按：
$S_{x o} (f) = {|H_{x a} (f)|}^{2} S_{a} (f)$
其中， $H_{x a} (f)$ 为频率函数。
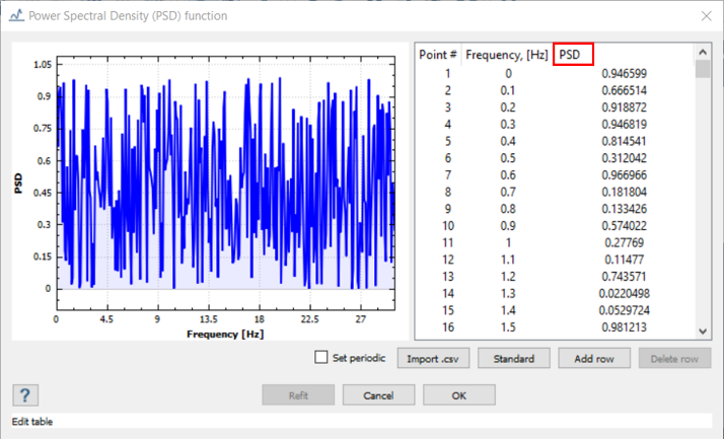
为了更好地理解，我们来举个例子，将以加速度为激励类型的基础激励作为随机响应分析的输入。
带振幅的基础激励用于定义频率响应分析的输入，因此加速度激励类型的单位可以是下面突出显示的任何单位：m/sec²、mm/sec²、cm/sec²、G、in/sec²
功率谱密度函数的单位取决于边界条件。在本例中，由于基础激励作为加速度给出，功率谱密度的单位为 (mm/s²)²/Hz。
图 1.