Tutorial: Inertia Relief Analysis

Tutorial Level: Beginner Define a force using components and run an analysis with inertia relief.

Overview

Inertia relief is a numerical method used for analyzing unconstrained structures. A typical example is an aircraft in steady flight where the lift, drag, and thrust loads are balanced by gravity acting on the mass of the total aircraft. This acceleration due to gravity is equal and opposite to the acceleration that would result for the unconstrained structure.

At a component level, with inertia relief it is possible to analyze a part in isolation if the loads at the interface points are known or can be measured/calculated and the part can be considered to be in static equilibrium.

This tutorial examines a motorcycle rear swing arm where the attaching structures — shock absorber, frame, and axle — are unknown, but the loads at the interface points have been provided. It comprises two main sections:
  • load setup
  • running inertia relief
The following table provides the loads that will be used in this tutorial. They are also shown throughout the tutorial as required.
Location Shock Pivot Axle
Force Fx N -2352 980 1372
Fy N 3211 -3700 489
Fz N -635 645 0
Moment Mx N*mm 0 -104867 -278
My N*mm 0 -188238 779
Mz N*mm 0 0 -7998

Apply a Component Force to the Shock Mount

  1. Press F7 to open the Demo Browser.
  2. Double-click the 0.0_swingarm_IR_FEA.x_b file to load it in the modeling window.
    This is a solid model of a single-part motorcycle swing arm.


  3. Make sure the display units in the Unit System Selector are set to MMKS (mm kg N s).
  4. On the Structure ribbon, click the Force button in the Loads tool group.


    Tip: To find and open a tool, press Ctrl+F. For more information, see Find and Search for Tools.
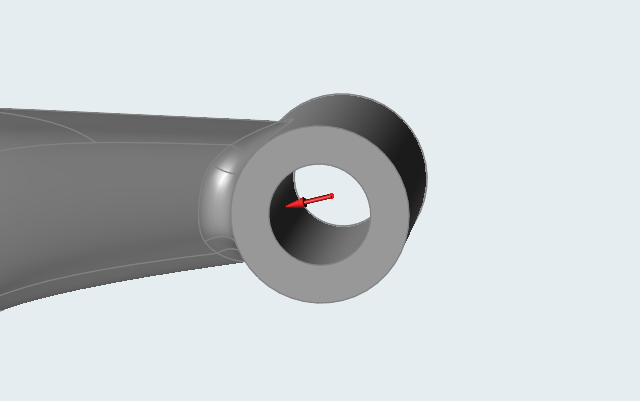
  5. Click to apply the force to the hole center of the shock mount.


  6. Click Vector Mode on the microdialog to switch to Component Mode, and then click the chevron to expand it.


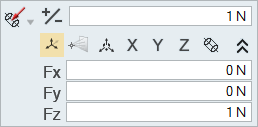
  7. Enter the following values:
    • Fx: -2352 N
    • Fy: 3211 N
    • Fz: -635 N


  8. Right-click and mouse through the check mark to exit, or double-right-click.

Apply a Component Force and Moment to the Swing Arm Pivot

  1. Zoom in on the swing arm pivot.
  2. On the Structure ribbon, select the Connectors tool.


    Tip: To find and open a tool, press Ctrl+F. For more information, see Find and Search for Tools.
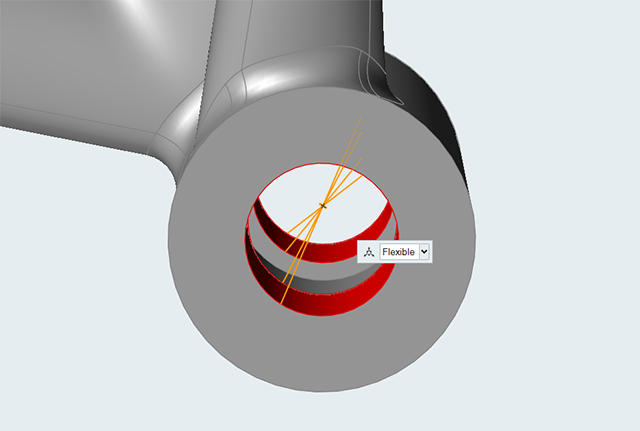
  3. Select the two faces as shown below to create a connector at the center of the hole:


  4. On the Structure ribbon, click the Force button in the Loads tool group.


  5. Click the connector at the center of the hole.
  6. Click Vector Mode on the microdialog to switch to Component Mode, and click the chevron to expand it.


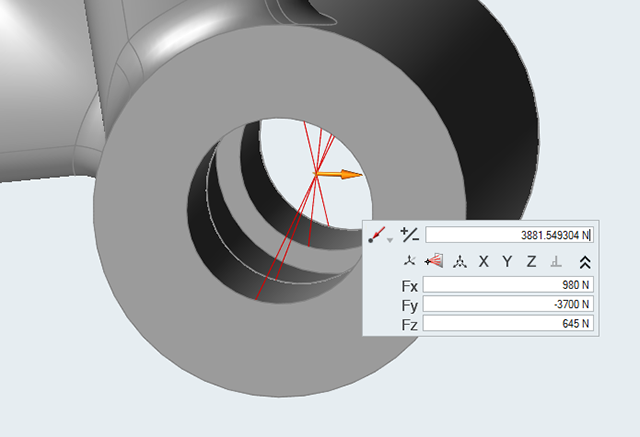
  7. Enter the following values:
    • Fx: 980 N
    • Fy: -3700 N
    • Fz: 645 N


  8. On the Structure ribbon, click the Torque button in the Loads tool group.


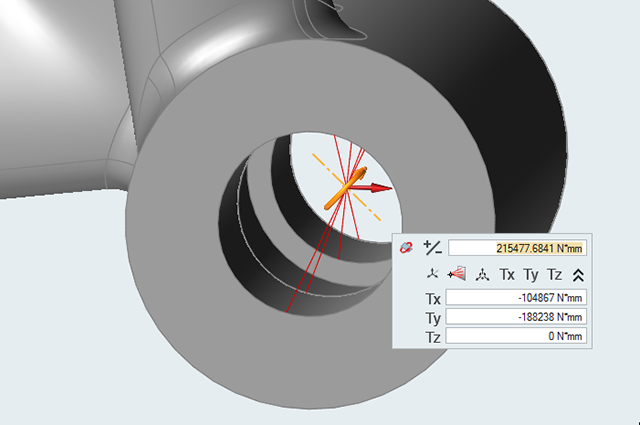
  9. Click the connector at the center of the hole.
  10. Click Vector Mode on the microdialog to switch to Component Mode, and click the 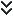chevron to expand it.


  11. Enter the following values:
    • Tx: -104867 N*mm
    • Ty: -188238 N*mm
    • Tz: 0 N*mm


  12. Right-click and mouse through the check mark to exit, or double-right-click.

Apply a Component Force and Moment to the Center of the Axle

  1. Zoom in on the center of the axle.


  2. On the Structure ribbon, click the Force button in the Loads tool group.


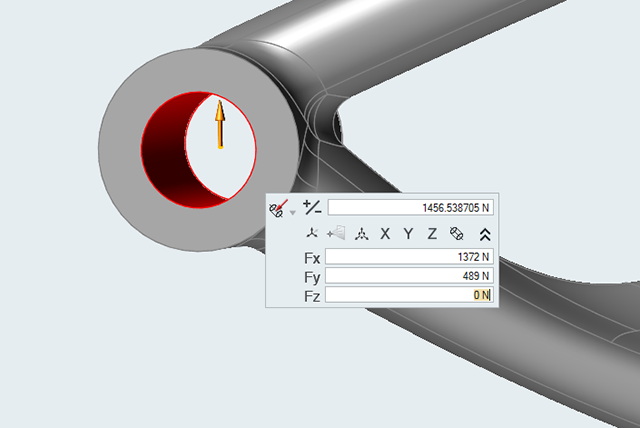
  3. Select the face as shown below to apply a force to the hole center of the axle.
  4. Click Vector Mode on the microdialog to switch to Component Mode, and click the chevron to expand it.


  5. Enter the following values:
    • Fx: 1372 N
    • Fy: 489 N
    • Fz: 0 N


  6. On the Structure ribbon, click the Torque button in the Loads tool group.


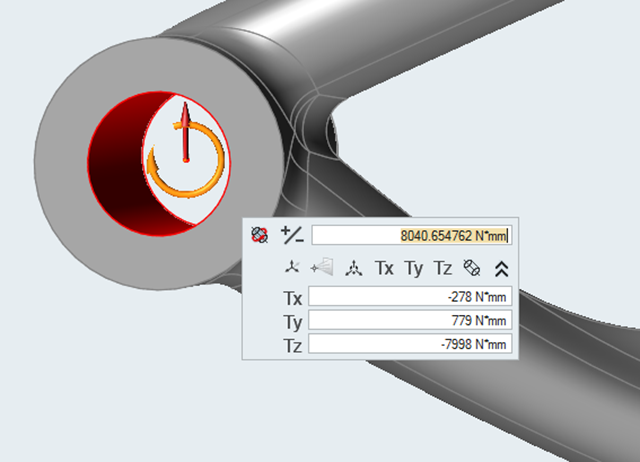
  7. Select the face shown below to apply a torque to the hole center of the axle.
  8. Click Vector Mode on the microdialog to switch to Component Mode, and click the chevron to expand it.


  9. Enter the following values:
    • Tx: -278 N*mm
    • Ty: 779 N*mm
    • Tz: -7998 N*mm


  10. Right-click and mouse through the check mark to exit, or double-right-click.

Run an Analysis with Inertia Relief

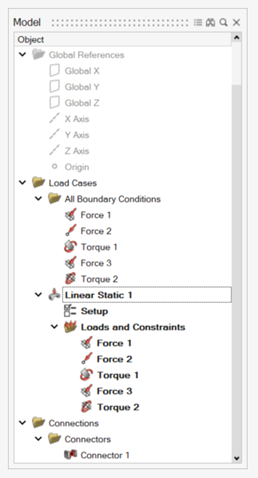
  1. Press F2 to open the Model Browser.
    Note that a default linear static load case has been created containing all the created loads.

  2. On the Structure ribbon, click the Run Analysis button in the Analyze tool group and ensure OptiStruct is selected as the solver.




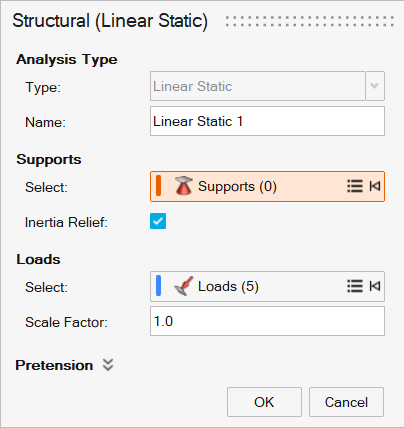
  3. In the Model Browser, double-click Setup under the Linear Static 1 heading.
    The Structural (Linear Static) guide panel is displayed.
  4. Select the Inertia Relief checkbox and then click OK.
  5. On the Structure ribbon, click the Run Analysis button in the Analyze tool group.


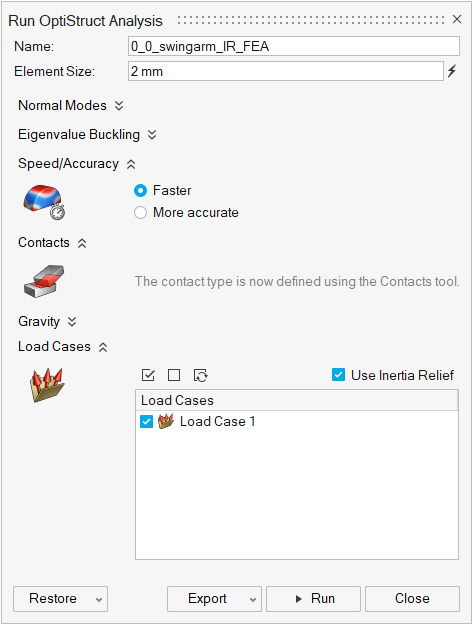
  6. Run the analysis using the following settings:
    1. Change the Element size to 3.0 mm.
    2. Set Speed to Faster.
    3. Select the Linear Static 1 load case.
    4. Click Run to perform the analysis.


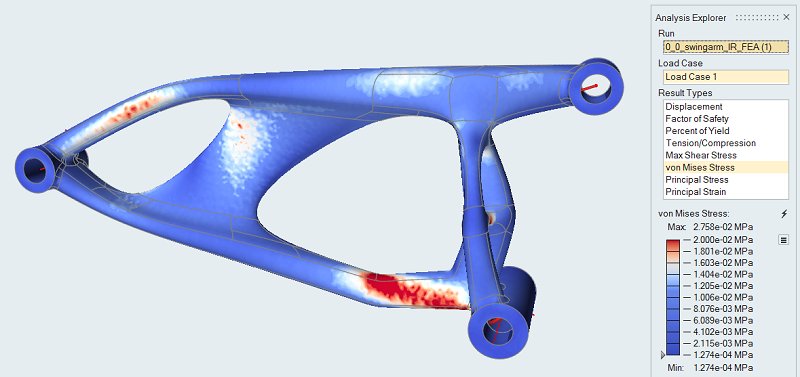
  7. When the run is complete, select it in the Run Status window and click View Now to view the results.
    Tip: You can also double-click the Results icon in the Model Browser to view results for a load case.

  8. In the Analysis Explorer, select von Mises Stress from the Result Types dropdown.
    Note: Even without supports, the analysis runs as any imbalance in the loads is reacted by the inertia forces.