The elastic-plastic behavior of isotropic material is modeled with user-defined
functions for work hardening curve.
The elastic portion of the material stress-strain curve is modeled using the elastic
modulus, E, and Poisson's ratio,
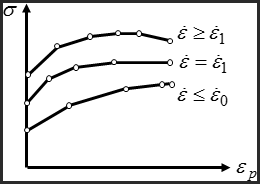
. The hardening behavior of the material is defined in function of
plastic strain for a given strain rate (Figure 1). An arbitrary number of material
plasticity curves can be defined for different strain rates. For a given strain rate, a
linear interpolation of stress for plastic strain change, can be used. This is the case of
LAW36 in Radioss. However, in LAW60 a quadratic interpolation of
the functions allows to better simulate the strain rate effects on the behavior of material
as it is developed in LAW60. For a given plastic strain, a linear interpolation of stress
for strain rate change is used. Compared to Johnson-Cook model (LAW2), there is no maximum
value for the stress. The curves are extrapolated if the plastic deformation is larger than
the maximum plastic strain. The hardening model may be isotropic, kinematic or a combination
of the two models as described in Cowper-Symonds Plasticity Model (LAW44). The material failure model is the same as in Zhao law.
For some kinds of steels the yield stress dependence to pressure has to be incorporated
especially for massive structures. The yield stress variation is then given
by:
(1)
Where,
is the pressure defined by
Stresses in Solids,
Equation 2. Drucker-Prager model described in
Drucker-Prager (LAW10 and LAW21) gives a nonlinear function for
. However, for steel type materials where the dependence to
pressure is low, a simple linear function may be considered:
(2)
Where,
-
- User-defined constant
-
- Computed pressure for a given deformed configuration
The principal strain rate is used for the strain rate definition:
(3)
For strain rate filtering, refer to Strain Rate Filtering.