Stresses in Solids
Principal Stresses
Since the stress tensor is symmetric, you can always find a proper orthogonal matrix, that is, a coordinate system that diagonalizes it:
The diagonal components are called the principal stresses and allow a 3D representation of the state of stress at a point.
Stress Invariants
Many of the constitutive models in Radioss are formulated in terms of invariants of the stress tensor. The most important are the first and second invariants, called pressure and von Mises stress after Richard von Mises.
The values of these functions remain invariant under transformation by a proper orthogonal matrix. If,
then,
Invariant Space
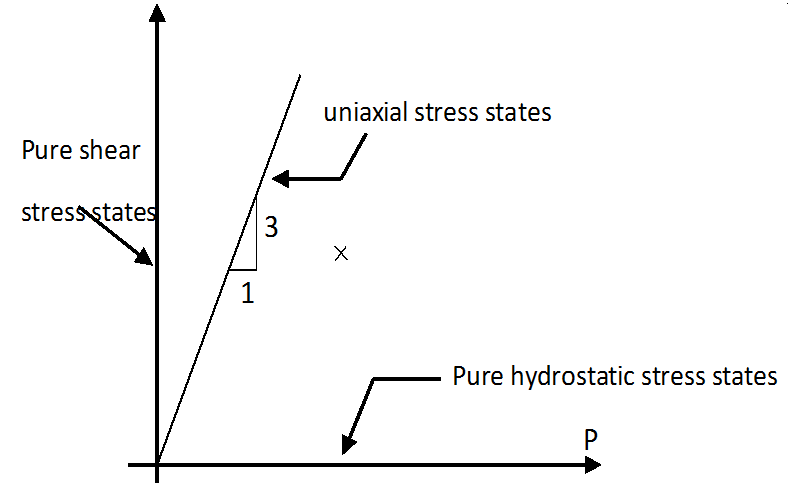
The horizontal axis corresponds to the hydrostatic loading, the vertical axes to pure shear. The line with tangent 1/3 is uniaxial compression. The line with tangent -1/3 is uniaxial tension.
Deviatoric Stresses
The pressure or first invariant is related to the change in volume of the solid. The deviation from a hydrostatic state of stress is linked to the change in shape. The stress deviator is defined as:
The second invariant becomes, in terms of the deviators:
A surface of constant von Mises stress in deviatoric space or principal deviatoric space is a sphere (in stress space it is a cylinder).