Drucker-Prager Constitutive Model (LAWS 10, 21 and 81)

Drucker-Prager (LAW10 and LAW21)

For materials, like soils and rocks, the frictional and dilatational effects are significant. In these materials, the plastic behavior depends on the pressure as the internal friction is proportional to the normal force.

Furthermore, for frictional materials, associative plasticity laws, in which the plastic flow is normal to the yield surface, are often inappropriate. Drucker-Prager ^¹ yield criterion uses a modified von Mises yield criteria to incorporate the effects of pressure for massive structures:

F = J_{2} - (A_{0} + A_{1} P + A_{2} P^{2})

Where,

$J_{2}$: Second invariant of deviatoric stress $J_{2} = \frac{1}{2} s_{i j} s_{i j}$
$P$: Pressure
$A_{0}$ , $A_{1}$ , $A_{2}$: Material coefficients

Figure 1 shows Equation 1 in the plane of $\sqrt{J_{2}}$ and $P$ . The criterion expressed in the space of principal stresses represents a revolutionary surface with an axis parallel to the trisecting of the space as shown in Figure 2. This representation is in contrast with the von Mises criteria where yield criterion has a cylindrical shape. Drucker-Prager criterion is a simple approach to model the materials with internal friction because of the symmetry of the revolution surface and the continuity in variation of normal to the yield surface.

For LAW10 pressure evaluation for EOS is described with /EOS/COMPACTION.

The pressure in the material is determined in function of volumetric strain for loading phase:

P = f (μ)

for loading $d μ > 0$

Where, $f$ is a user-defined (LAW21) or a cubic polynomial function (LAW10). For unloading phase, if the volumetric strain has a negative value, a linear relation is defined as:

P = C_{1} μ

for unloading $d μ < 0$ and $μ < 0$

For unloading with a positive volumetric strain, another linear function may be used:

P = B μ

for unloading $d μ < 0$ and $μ > 0$

In Radioss extended Drucker-Prager model is used in LAW10 and LAW21. Neither of these laws can reproduce the mono-dimensional behavior. In addition, no viscous effect is taken into account.

Figure 1. Yield Criteria in the Plane of $\sqrt{J_{2}}$ and P

Figure 2. Drucker-Prager Yield Criteria in Space of Principal Stresses

Figure 3. Material Pressure Variation in Function of Volumetric Strain

Drucker-Prager Constitutive Model with Cap (LAW81)

Yield Surface

The Drucker-Prager yield surface is:

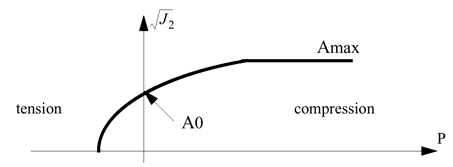
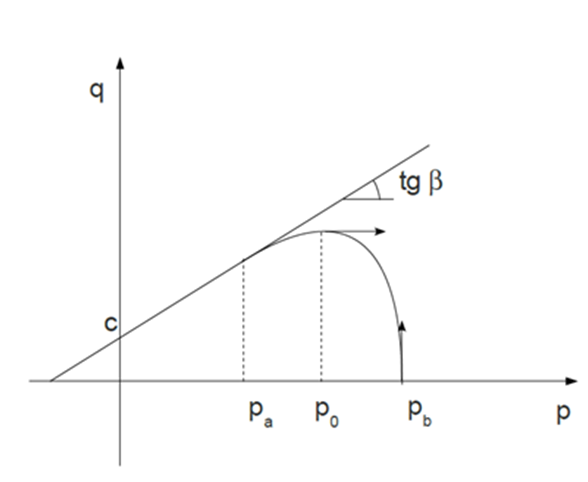
F = q - r_{c} (p) \cdot (p \tan β + c) = 0

Cap hardening considered in this material law in $p_{a} < p < p_{b}$ is described with:

r_{c} (p) = \sqrt{1 - {(\frac{p - p_{a}}{p_{b} - p_{a}})}^{2}}

In lower compression or tension $p \leq p_{a}$ , then linear yield surface will be considered with:

r_{c} (p) = 1

Where,

$q$: von Mises stress; $q^{2} = 3 J_{2} = \frac{3}{2} s_{i j}^{2}$
$p$: Pressure; $p = - \frac{1}{3} σ_{i j} = - \frac{1}{3} I_{1}$
$s_{i j}$: Deviatoric stress; $s_{i j} = σ_{i j} + p δ_{i}^{j}$
$_{c}$: Cohesion
$β$: Friction angle
$p_{0}$: Pressure value; $\frac{\partial F}{\partial p} (p_{0}) = 0$

Plastic Flow

Plastic flow is governed by the non-associated flow potential $G$ defined as:

If $p \leq p_{a}$

G = q - p \cdot \tan ψ = 0

If $p_{a} < p \leq p_{0}$

G = q - \tan ψ (p - \frac{{(p - p_{a})}^{2}}{2 (p_{0} - p_{a})}) = 0

If $p > p_{0}$ (example, the flow becomes associated on the cap)

G = F

The plastic potential is continuous as you have $\frac{\partial G}{\partial p} (p_{0}) = \frac{\partial F}{\partial p} (p_{0}) = 0$ .

By definition the plastic flow is normal to the flow potential.

d ε_{i j}^{p} = d Λ \cdot \frac{\partial G}{\partial σ_{i j}}

The scalar $d Λ$ will be determined in order to satisfy consistency and experimental hardening/softening.

Hardening/Softening

The cap is defined by only one parameter $p_{b}$ , assume that $p_{a}$ evolves according to:

\frac{p_{a}}{p_{b}} = \frac{p_{a 0}}{p_{b 0}} = α

Where,

$p_{a 0}$ and $p_{b 0}$: Initial value of $p_{a}$ and $p_{b}$

The evolution of

p_{b}

depends on

ε_{v}^{p} = - ε_{i i}^{p}

via a curve given in input fct_ID_pb.

Note: The same sign conversion for

ε_{v}^{p}

and

p_{b}

, which is positive in compression is considered.

Shear yielding has an effect on $p_{b}$ , which depends on the possible dilantancy imposed by the flow rule. An option to prevent this phenomenon is provided, for example, for rocks (cap softening deactivation flag I_soft).
$p_{a}$ is derived from $p_{b}$ via Equation 12
If softening is allowed, the condition $p_{a} > 0$ is imposed, otherwise, $d ε_{v}^{p} \geq 0$

Derive Stress-Strain Relationships

Considering bulk and shear moduli $K$ and $μ$ , write the relationship between stress and elastic strain deviatoric tensors and and between pressure and volumetric strain and its plastic component.

d s_{i j} = 2 μ (d e_{i j} - d e_{i j}^{p})

d p = - K (d ε_{i i} - d ε_{i i}^{p}) = - K (d ε_{i i} - d ε_{i i}^{p})

Note that,

\frac{\partial G}{\partial σ_{i j}} = - \frac{1}{3} \frac{\partial G}{\partial p} δ_{i}^{j} + \frac{3}{2 q} s_{i j}

\frac{\partial F}{\partial s_{i j}} = \frac{\partial G}{\partial s_{i j}} = \frac{3}{2 q} s_{i j}

You can relate the increment of the plastic volumetric strain $d ε_{v}^{p}$ and the equivalent plastic strain $d ε_{d}^{p}$ and $d Λ$ .

d ε_{v}^{p} = d Λ \frac{\partial G}{\partial p}

and $d ε_{d}^{p} = d Λ \frac{\partial G}{\partial q}$ with $\frac{\partial G}{\partial q} = 1$ .

and solving for $d Λ$ from Equation 11, Equation 14, Equation 16 and Equation 17, you obtain,

d Λ = \frac{1}{h} (\frac{\partial F}{\partial s_{i j}} 2 μ d e_{i j} - \frac{\partial F}{\partial p} K d ε_{i i})

With $h = 3 μ + K \frac{\partial F}{\partial p} \frac{\partial G}{\partial p} - \frac{\partial F}{\partial c} \frac{d c}{d ε_{d}^{p}} - \frac{\partial G}{\partial p} \frac{\partial F}{\partial p_{b}} \frac{d p_{b}}{d ε_{v}^{p}}$

You can then compute all terms in Equation 18.

If $p \leq p_{a}$ , then $\frac{\partial F}{\partial p} = - \tan β$ , $\frac{\partial F}{\partial c} = - 1$ , $\frac{\partial F}{\partial p_{b}} = 0$ .

If $p \geq p_{a}$ , then

\frac{\partial F}{\partial p} = - (\tan β r_{c} + \frac{d r_{c}}{d p} (p \tan β + c))

$\frac{\partial F}{\partial c} = - r_{c} (p)$

and $\frac{\partial F}{\partial p_{b}} = \frac{- p (p - p_{a})}{r_{c} p_{b} {(p_{b} - p_{a})}^{2}} (p \tan β + c)$

If $p \leq p_{a}$ , then $\frac{\partial G}{\partial p} = - \tan ψ$

If $p_{a} \leq p \leq p_{0}$ , then

\frac{\partial G}{\partial p} = - \tan ψ \frac{(p_{0} - p)}{(p_{0} - p_{a})}

If $p \geq p_{0}$ , then $\frac{\partial F}{\partial p} = \frac{\partial G}{\partial p}$

Finally, $\frac{d q}{d p} = 0$ gives

p_{0} = p_{a} + \frac{- (p_{a} \tan β + c) + \sqrt{{(p_{a} \tan β + c)}^{2} + 8 {[\tan β (p_{b} - p_{a})]}^{2}}}{4 \tan β}

When $p < p_{0}$ and $\frac{\partial G}{\partial p} < 0$ leads to softening of the cap. If the no-softening cap flag is set, the last term in Equation 14 is irrelevant. To achieve this, set $\frac{\partial F}{\partial p_{b}} = 0$ and impose on the hardening parameter $d ε_{v}^{p}$ not decrease, although there is some volumetric plastic flow $d ε_{v}^{p}$ .

For $p \to p_{b}$ , $\frac{d r_{c}}{d p} \to \infty$ , $d Λ \to \infty$ , so that $d ε_{v}^{p}$ is undetermined in Equation 17.

In this case, a special treatment needs to be performed; at first order, the deviatoric terms are neglected.

d ε_{v}^{p} = - d ε_{v} (\frac{K}{K + \frac{d p_{b}}{d ε_{v}^{p}}})

d e_{i j}^{p} = 0

Elastic Properties

Yielding the cap actually models the compaction process. The elastic properties should thus increase when the porosity decreases, that is, $ε_{v}^{p}$ increases.

The variation of

K

and

μ

with

ε_{v}^{p}

are determined by two functions given in input.

Note: Typically, when variable elastic properties are used, the hardening parameter

ε_{v}^{p} = \int d ε_{v}^{p}

and the volumetric deformation after full unloading are not consistent.

Porosity Model

The porosity model is inspired by ^² and assumes the soils are made of elastic grains with voids and is for low energies when the soil is not fully compacted. For a fully compacted soil at high energy, an equation of state should be used. In this material law, the variation of the volume of voids has an elastic part due to the elastic deformation of the skeleton and a plastic part which corresponds to the rearrangement of grains which induces compaction upon pressure loadings and dilatancy when undergoing shear loadings.

Note: The presence of air is not part of this model. The porosity is defined so that it represents the volume fraction of voids, with respect to the total reference volume.

n = \frac{V_{v o i d}}{V_{t o t a l}}

In the elastic case, the void volume does not change. However, in the plastic case, the porosity change is defined by:

n = 1 - (1 - n_{0}) e^{ε_{v}^{p} - ε_{v 0}^{p}}

The initial state of the pores is defined by the initial porosity, initial saturation, and initial pore pressure. The saturation is defined as the ratio of the volume of the water to the volume in the void:

S = \frac{V_{w a t e r}}{V_{v o i d}}

The above voids can be partly or totally filled with water. In soil mechanics, when the soil is not saturated $S < 1$ the only effect of water is its weight and mass so the water pressure $u = 0$ ; the mechanical properties are then the same as the drained soil. When the soil is saturated $S \geq 1$ , the water pressure $u$ is taken into account using Terzaghi’s assumption. ^³ The total pressure is $p = p^{'} + u$ , where $p$ is the effective pressure in the structure that has the voids. Also, assume the initial water pressure does not exceed the initial pressure in the skeleton.

The average density of the void can be calculated as the mass of the water divided by the volume of the void:

ρ_{v o i d} = \frac{m_{w a t e r}}{V_{v o i d}}

Next, define:

μ_{w} = \frac{ρ_{v o i d}}{ρ_{w 0}} - 1

Where, $ρ_{w 0}$ is the initial density of the water.

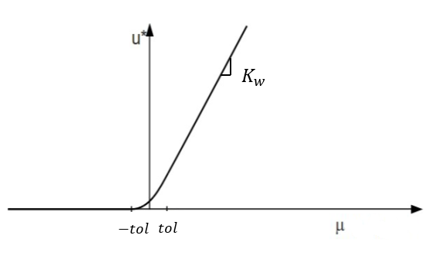
For stability reasons, a viscousity term is added.

If $μ_{w} > - t o l then u_{v i s} = - α_{v} \sqrt{K_{w} ρ} {(V o l)}^{\frac{1}{3}} ε_{v}$ and is added to $u^{*}$ .

For a smoother transition, define:

\begin{array}{l} If μ_{w} < - t o l : u^{*} = 0 \\ If | μ_{w} | < t o l : u^{*} = \frac{K_{w}}{4 t o l} {(μ_{w} + t o l)}^{2} \\ If μ_{w} > t o l : u^{*} = K_{w} μ_{w} \end{array}

Where,

K_{w}

is the water bulk modulus.

The cap is then modified by adding a purely von Mises region for

p_{0} \leq p^{'} \leq p_{0} + u^{*}

¹ Drucker D. and Prager W., Soil mechanics and plastic analysis of limit design, Quart. Appl. Math., Vol. 10, 157-165, 1952.

² R. Kohler and G. Hofstetter, A cap model for partially saturated soils, Wiley & Sons, 2007

³ Karl Terzaghi, Theoretical Soil Mechanics, Wiley & Sons, 1943