Brittle Damage: Reinforced Concrete Material (LAW24)

The model is a continuum, plasticity-based, damage model for concrete. It assumes that the main two failure mechanisms are tensile cracking and compressive crushing of the concrete material.

The material law will enable to formulate the brittle elastic - plastic behavior of the reinforced concrete.

The input data for concrete are:
E c
Young's modulus
32000 MPa
Vc
Poisson's ratio
0.2
fc
Uniaxial compressive strength
32 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
fi/fc
Tensile strength ratio
Default = 0.1
fb/fc
Biaxial strength ratio
Default = 1.2
f2/fc
Confined strength ratio
Default = 4.0
s0/fc
Confining stress ratio
Default = 1.25

Experimental results enable to determine the material parameters. This can be done by in-plane unidirectional and bi-axial tests as shown in Figure 2. The expression of the failure surface is in a general form as:

f = r − k ( σ m , k 0 ) ⋅ r f = 0

Where,
J 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsamaaBa aaleaacaaIYaaabeaaaaa@37AD@
Second invariant of stress
Where, r = 2 J 2 = 2 3 σ V M
σ m = I 1 3
Mean stress

A schematic representation of the failure surface in the principal stress space is given in Figure 2. The yield surface is derived from the failure envelope by introducing a scale factor k ( σ m , k 0 ) . The meridian planes are presented in Figure 3.

The steel directions are defined identically to material LAW14 by a TYPE6 property set. If a property set is not given in the element input data, r, s, θ are taken respectively as direction 1, 2, 3. For quad elements, direction 3 is taken as the θ direction.

Steel data properties are:
E MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyraaaa@36C1@
Young's modulus
σ y
Yield strength
E t MathType@MTEF@5@5@+= feaahGart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyramaaBa aaleaacaWG0baabeaaaaa@37E6@
Tangent modulus
α 1
Ratio of reinforcement in direction 1
α 2
Ratio of reinforcement in direction 2
α 3
Ratio of reinforcement in direction 3
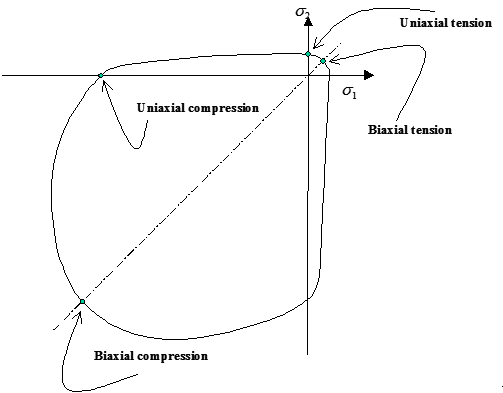
Figure 1. Failure Surface in Plane Stress


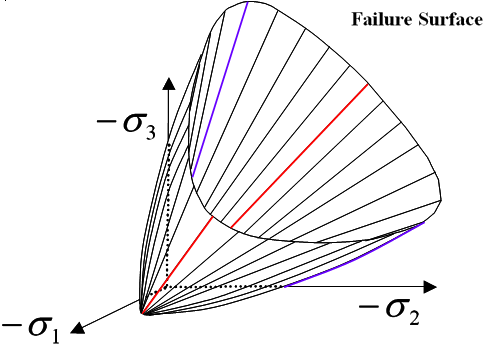
Figure 2. Failure Surface in Principal Stress Space


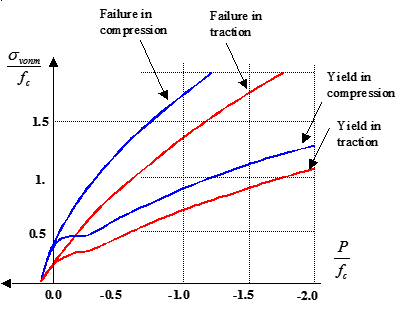
Figure 3. Meridians of Failure and Yield Surfaces