Deviatoric Stress Calculation
With the stress being separated into deviatoric and pressure (hydrostatic) stress (Stresses in Solids), it is the deviatoric stress that is responsible for the plastic deformation of the material. The hydrostatic stress will either shrink or expand the volume uniformly, that is, with proportional change in shape. The determination of the deviatoric stress tensor and whether the material will plastically deform requires a number of steps.
Perform an Elastic Calculation
The deviatoric stress is time integrated from the previous known value using the strain rate to compute an elastic trial stress:
Where, is the shear modulus.
This relationship is Hooke's Law, where the strain rate is multiplied by time to give strain.
Compute von Mises Equivalent Stress and Current Yield Stress
Depending on the type of material being modeled, the method by which yielding or failure is determined will vary. The following explanation relates to an elastoplastic material (LAW2).
The von Mises equivalent stress relates a three dimensional state of stress back to a simple case of uniaxial tension where material properties for yield and plasticity are well known and easily computed.
The von Mises stress, which is strain rate dependent, is calculated using the equation:
The flow stress is calculated from the previous plastic strain:
For material laws 3, 4, 10, 21, 22, 23 and 36, Equation 3 is modified according to the different modeling of the material curves.
Plasticity Check
The state of the deformation must be checked.
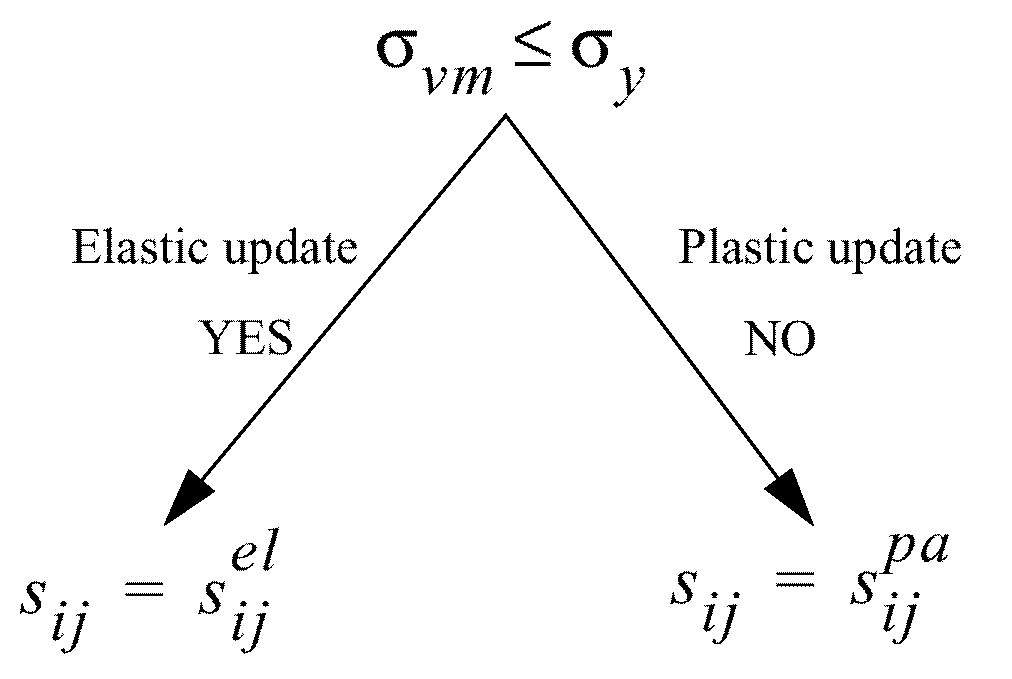
The plasticity algorithm used is due to Mendelson. 1
Compute Hardening Parameter
The hardening parameter is defined as the slope of the strain-hardening part of the stress-strain curve:
This is used to compute the plastic strain at time :
This plastic strain is time integrated to determine the plastic strain at time :
The new flow stress is found using:
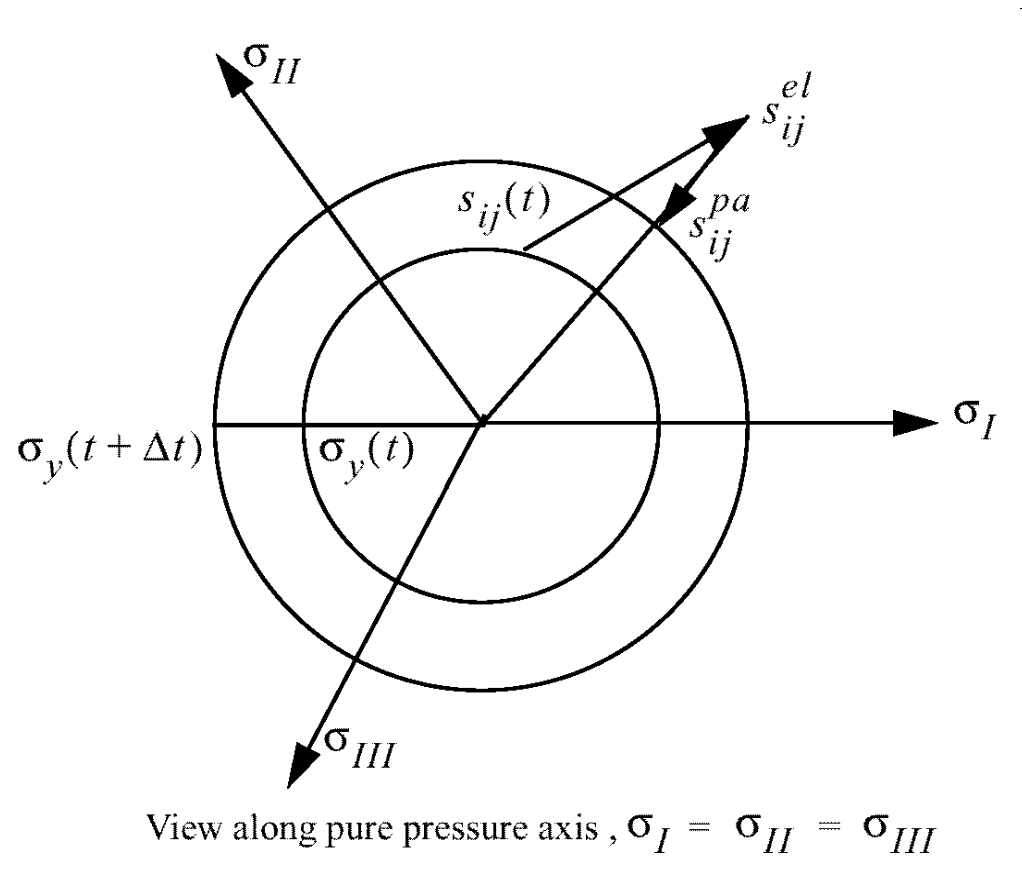
Radial Return
There are many possible methods for obtaining from the trial stress. The most popular method involves a simple projection to the nearest point on the flow surface, which results in the radial return method.
Plasticity: Theory and Application, MacMillan Co., New York, 1968.