Integrated Beam Elements (TYPE 18)
Beam type /PROP/TYPE18 uses a shear beam theory or Timoshenko formulation like /PROP/TYPE3, but the section inputs (area, inertia) can be default values and can also be discretized by sub-sections; numerical integrations are used to calculate internal forces.
- No deformation of the cross-section in its plane.
- No warping of the cross-section out of its plane
Using these assumptions, transverse shear is always considered.
Local Coordinate System
The properties describing a beam element are all defined in a local coordinate system.
This coordinate system is the same as /PROP/TYPE3 and can be seen in Figure 1. Nodes 1 and 2 of the element are used to define the local X axis, with the origin at node 1. The local Y axis is defined using node 3, which lies in the local XY plane, along with nodes 1 and 2. The Z axis is determined from the vector cross product of the positive X and Y axes.
In case Node 3 is not defined, Nodes 1 and 2 of the element are used to define the local X axis, with the origin at node 1. Local XY plane is defined using local X axis and Global Z axis (or Global Y axis, if local X is parallel to global Z). The local Y axis is determined from the vector cross product of the positive Z and X axes.
The local Y direction is first defined at time and its position is updated at each cycle, taking into account the rotation of the X axis. The Z axis is always orthogonal to the X and Y axes.
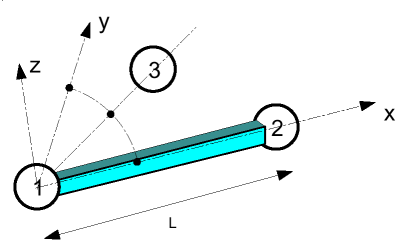
Figure 1. Beam Element Local Axis
Beam Element Geometry
- = 1
- Pre-defined rectangular section
- = 2
- Pre-defined circular section
- = 3
- Pre-defined rectangular section with Gauss-Lobatto quadrature
- = 4
- Pre-defined circular section with Gauss-Lobatto quadrature
- = 5
- Pre-defined circular section
Minimum Time Step
- Speed of sound,
Beam Element Behavior
- Constant strain rate at local axis x
- Curvature rate