Pulley Type Spring Elements (TYPE12)
Pulley type springs are defined by TYPE12 element property. A general representation can be seen in Figure 1. It is defined with three nodes, where node 2 is located at the pulley position. Other properties such as stiffness, damping, nonlinear and plastic effects are the same as for the other spring types, and are defined using the same format.
A deformable "rope" joins the three nodes, with the mass distribution as follows: one quarter at node 1; one quarter at node 3 and one half at node 2.
Coulomb friction can be applied at node 2, which may also take into account the angle between the two rope strands.
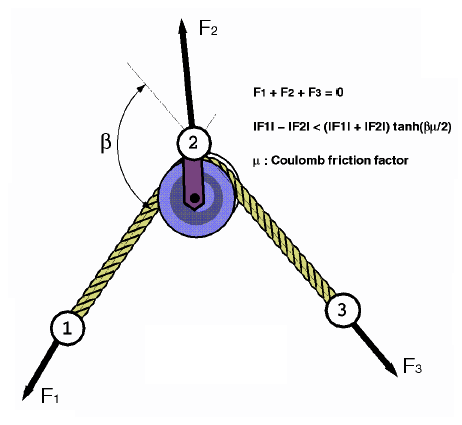
Figure 1. Pulley Type Spring Element Representation
Time Step
This is the same as for TYPE4 spring elements, except that the stiffness is replaced with twice the stiffness to ensure stability with high friction coefficients.
Linear Spring
See Linear Spring; the explanation is the same as for spring TYPE4.
Nonlinear Elastic Spring
See Nonlinear Elastic Spring; the explanation is the same as for spring TYPE4.
Nonlinear Elasto-Plastic Spring - Isotropic Hardening
See Nonlinear Elasto-plastic Spring: Isotropic Hardening; the explanation is the same as for spring TYPE4.
Nonlinear Elasto-Plastic Spring - Decoupled Hardening
See Nonlinear Elasto-plastic Spring: Decoupled Hardening; the explanation is the same as for spring TYPE4.
Nonlinear Dashpot
See Nonlinear Dashpot; the explanation is the same as for spring TYPE4.
Friction Effects

Figure 2.
Forces without Friction
- Total rope elongation = with
- Rope stiffness
- Rope equivalent viscous damping
Forces with Coulomb Friction
- Elongation of strand 1-2
- Elongation of strand 2-3