Home
Theory Manual
This manual provides detailed information about the theory used in the Altair Radioss Solver.
Large Displacement Finite Element Analysis Theory Manual
Element Library
Radioss element library contains elements for one, two or three dimensional problems.
Truss Elements (TYPE2)

Welcome
What's New
View new features for Radioss 2024.1.
Overview
Radioss^® is a leading explicit finite element solver for crash and impact simulation.
Tutorials
Discover Radioss functionality with interactive tutorials.
User Guide
This manual provides details on the features, functionality, and simulation methods available in Altair Radioss.
Reference Guide
This manual provides a detailed list of all the input keywords and options available in Radioss.
Example Guide
This manual presents examples solved using Radioss with regard to common problem types.
Verification Problems
This manual presents solved verification models.
Frequently Asked Questions
This section provides quick responses to typical and frequently asked questions regarding Radioss.
Theory Manual
This manual provides detailed information about the theory used in the Altair Radioss Solver.
- Large Displacement Finite Element Analysis Theory Manual
  - Introduction
    Nonlinear finite element analyses confront users with many choices. An understanding of the fundamental concepts of nonlinear finite element analysis is necessary if you do not want to use the finite element program as a black box. The purpose of this manual is to describe the numerical methods included in Radioss.
  - Basic Equations
  - Finite Element Formulation
  - Dynamic Analysis
  - Element Library
    Radioss element library contains elements for one, two or three dimensional problems.
    - Solid Hexahedron Elements
    - Solid Tetrahedron Elements
    - Shell Elements
    - Solid-Shell Elements
    - Truss Elements (TYPE2)
    - Beam Elements (TYPE3)
    - One Degree of Freedom Spring Elements (TYPE4)
    - General Spring Elements (TYPE8)
    - Pulley Type Spring Elements (TYPE12)
    - Beam Type Spring Elements (TYPE13)
    - Integrated Beam Elements (TYPE 18)
      Beam type /PROP/TYPE18 uses a shear beam theory or Timoshenko formulation like /PROP/TYPE3, but the section inputs (area, inertia) can be default values and can also be discretized by sub-sections; numerical integrations are used to calculate internal forces.
    - Multistrand Elements (TYPE28)
      Multistrand elements are n-node springs where matter is assumed to slide through the nodes.
    - Spring Type Pretensioners (TYPE32)
  - Kinematic Constraints
    Kinematic constraints are boundary conditions that are placed on nodal velocities. They are mutually exclusive for each degree of freedom (DOF), and there can only be one constraint per DOF.
  - Linear Stability
    The stability of solution concerns the evolution of a process subjected to small perturbations. A process is considered to be stable if small perturbations of initial data result in small changes in the solution. The theory of stability can be applied to a variety of computational problems.
  - Interfaces
    Interfaces solve the contact and impact conditions between two parts of a model.
  - Material Laws
    A large variety of materials is used in the structural components and must be modeled in stress analysis problems. For any kind of these materials a range of constitutive laws is available to describe by a mathematical approach the behavior of the material.
  - Monitored Volume
    An airbag is defined as a monitored volume. A monitored volume is defined as having one or more 3 or 4 node shell property sets.
  - Static
    Explicit scheme is generally used for time integration in Radioss, in which velocities and displacements are obtained by direct integration of nodal accelerations.
  - Radioss Parallelization
    The performance criterion in the computation was always an essential point in the architectural conception of Radioss. At first, the program has been largely optimized for the vectored super-calculators like CRAY. Then, a first parallel version SMP made possible the exploration of shared memory on processors.
- ALE, CFD and SPH Theory Manual
- Appendix A: Basic Relations of Elasticity
User Subroutines
This manual describes the interface between Altair Radioss and user subroutines.

View All Altair HyperWorks Help

Truss Elements (TYPE2)

Truss elements are simple two node linear members that only take axial extension or compression. Figure 1 shows a truss element.

Figure 1. Truss Element

Property Input

The only property required by a truss element is the cross-sectional area. This value will change as the element is deformed. The cross sectional area is computed using:

A r e a (t) = \frac{A r e a (t - Δ t)}{{(1 - v {\dot{ε}}_{x} Δ t)}^{2}}

Where,

$ν$: Poisson's ratio defined in the material law

Stability

Determining the stability of truss elements is very simple. The characteristic length is defined as the length of the element, that is, the distance between N1 and N2 nodes.

Δ t \leq \frac{L (t)}{C}

Where,

$L (t)$: Current truss length
$C = \sqrt{\frac{E}{ρ}}$: Sound speed

Rigid Body Motion

The rigid body motion of a truss element as shown in Figure 2 shows the different velocities of nodes 1 and 2. It is the relative velocity difference between the two nodes that produces a strain in the element, namely e_x.

Figure 2. Truss Motion

Strain

The strain rate, as shown in Figure 2, is defined as:

{\dot{ε}}_{x} = \frac{\partial v_{x}}{\partial x} = \frac{\partial (\vec{V} \cdot {\vec{e}}_{x})}{\partial x}

Material Type

A truss element may only be assigned two types of material properties. These are TYPE1 and TYPE2, elastic and elasto-plastic properties, respectively.

Force Calculation

The calculation of forces in a truss element is performed by explicit time integration:

A r e a (t) = \frac{A r e a (t - Δ t)}{{(1 - v {\dot{ε}}_{x} Δ t)}^{2}}

A generalized force-strain graph can be seen in Figure 3. The force rate under elastic deformation is given by:

{\dot{F}}_{x} = E A {\dot{ε}}_{x}

Where,

$E$: Elastic modulus
$A$: Cross-sectional area

In the plastic region, the force rate is given by:

{\dot{F}}_{x} = E_{t} A {\dot{ε}}_{x}

Where,

$E_{t}$: Gradient of the material curve at the deformation point

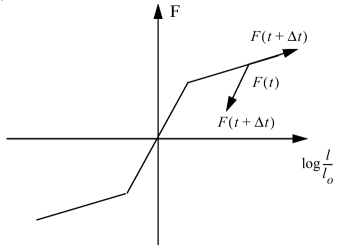
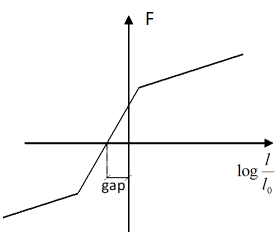
Figure 3. Force-Strain Relationship. (a) without gap; (b) with gap

Figure 3. Force-Strain Relationship. (a) without gap; (b) with gap

In a general case, it is possible to introduce a gap distance in the truss definition. If gap is not null, the truss is activated when the length of the element is equal to the initial length minus the gap value. This results a force-strain curve shown in Figure 3(b).